【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac,
其中正确的有( )

A.1个 B.2个 C.3个 D.4个
参考答案:
【答案】D
【解析】
试题分析:①将x=﹣2代入y=ax2+bx+c,可以结合图象得出x=﹣2时,y<0;
②由抛物线开口向下,可得a<0;由图象知抛物线的对称轴大于﹣1,则有x=![]() >﹣1,即可得出2a﹣b<0;
>﹣1,即可得出2a﹣b<0;
③已知抛物线经过(﹣1,2),即a﹣b+c=2(1),由图象知:当x=1时,y<0,即a+b+c<0(2),联立(1)(2),可得a+c<1;
④由抛物线的对称轴大于﹣1,可知抛物线的顶点纵坐标应该大于2,结合顶点的纵坐标与a<0,可以得到b2+8a>4ac.
解:①由函数的图象可得:当x=﹣2时,y<0,即y=4a﹣2b+c<0,故①正确;
②由函数的图象可知:抛物线开口向下,则a<0;抛物线的对称轴大于﹣1,即x=![]() >﹣1,得出2a﹣b<0,故②正确;
>﹣1,得出2a﹣b<0,故②正确;
③已知抛物线经过(﹣1,2),即a﹣b+c=2(1),由图象知:当x=1时,y<0,即a+b+c<0(2),
联立(1)(2),得:a+c<1,故③正确;
④由于抛物线的对称轴大于﹣1,所以抛物线的顶点纵坐标应该大于2,即:![]() >2,由于a<0,所以4ac﹣b2<8a,即b2+8a>4ac,故④正确,
>2,由于a<0,所以4ac﹣b2<8a,即b2+8a>4ac,故④正确,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】认真阅读下面的材料,完成有关问题.
材料:在学习绝对值时,老师教过我们绝对值的几何含义,如
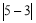 表示
表示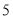 、
、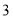 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;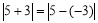 ,所以
,所以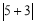 表示
表示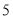 、
、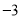 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离; ,所以
,所以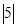 表示
表示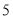 在数轴上对应的点到原点的距离.
在数轴上对应的点到原点的距离.一般地,点
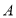 、点
、点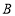 在数轴上分别表示有理数
在数轴上分别表示有理数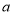 、
、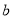 ,那么点
,那么点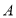 、点
、点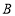 之间的距离可表示为
之间的距离可表示为 .
.(1)点
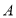 、
、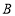 、
、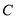 在数轴上分别表示有理数
在数轴上分别表示有理数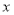 、
、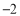 、
、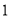 ,那么点
,那么点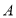 到点
到点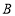 的距离与点
的距离与点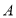 到点
到点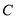 的距离之和可表示为__________(用含绝对值的式子表示).
的距离之和可表示为__________(用含绝对值的式子表示).(2)利用数轴探究:
①满足
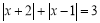 的
的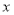 的取值范围是__________.
的取值范围是__________.②满足
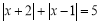 的
的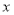 的所有值是__________.
的所有值是__________.③设
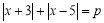 ,当
,当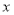 的值取在不小于
的值取在不小于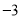 且不大于
且不大于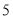 的范围时,
的范围时,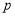 的值是不变的,而且是
的值是不变的,而且是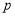 的最小值,这个最小值是_____.
的最小值,这个最小值是_____.(3)拓展:
①
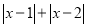 的最小值为__________.
的最小值为__________.②
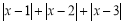 的最小值为__________.
的最小值为__________.③
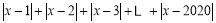 的最小值为__________,此时
的最小值为__________,此时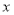 的取值范围为__________.
的取值范围为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,点
中,点 的坐标为(0,4),线段
的坐标为(0,4),线段 的位置如图所示,其中点
的位置如图所示,其中点 的坐标为(
的坐标为( ,
, ),点
),点 的坐标为(3,
的坐标为(3, ).
).
(1)将线段
 平移得到线段
平移得到线段 ,其中点
,其中点 的对应点为
的对应点为 ,点
,点 的对应点为点
的对应点为点 .
.①点
 平移到点
平移到点 的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;②点
 的坐标为 .
的坐标为 .(2)在(1)的条件下,若点
 的坐标为(4,0),连接
的坐标为(4,0),连接 ,画出图形并求
,画出图形并求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为
 ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.分数段
频数
百分比

38
0.38

0.32

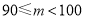
10
0.1
合计
100
1
书法作品比赛成绩频数直方图

根据上述信息,解答下列问题:
(1)请你把表中空白处的数据填写完整.
(2)请补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级的幅数.
-
科目: 来源: 题型:
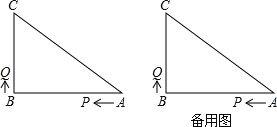
查看答案和解析>>【题目】如图,在△ABC中,∠B=90°,AB=8厘米,BC=6厘米,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动速度为1厘米/秒,点Q从点B开始沿B→C→A方向运动速度为2厘米/秒,若它们同时出发,设出发的时间为t秒.
(1)求出发2秒后,PQ的长;
(2)点Q在CA边上运动时,当△BCQ成为等腰三角形时,求点Q的运动时间.
相关试题

