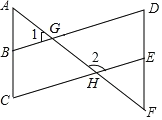
【题目】如图,已知AF分别与BD、CE交于点G、H,其中∠1+∠2=180°.
(1)判断BD和CE有怎样的位置关系,并说明理由;
(2)若∠A=∠F,探索∠C与∠D的数量关系,并证明你的结论.
参考答案:
【答案】(1)BD∥CE,理由见解析;(2)![]() ,理由见解析;
,理由见解析;
【解析】
(1)根据对顶角相等得出∠DGH=∠1,再由平行线的判定定理即可得出结论;
(2)先根据BD∥CE得出∠D=∠CEF,再由∠A=∠F得出AC∥DF,据此可得出结论.
(1)证明:∵∠1=∠DGH,∠1+∠2=180°,
∴∠DGH+∠2=180°,
∴BD∥CE;
(2)∠C=∠D.
理由:∵BD∥CE,
∴∠D=∠CEF.
∵∠A=∠F,
∴AC∥DF,
∴∠C=∠CEF,
∴∠C=∠D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上。

(1)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(2)若连接AA′、BB′,则这两条线段之间的关系是________________;
(3)在图中画出△ABC的高CD;
(4)△A′B′C′的面积为________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A.
 B.
B.  C.
C.
 D.
D. 


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).

(1)图2中的阴影部分的面积为 ;
(2)观察图2请你写出(a+b)2、(ab)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若m+n=5,mn=4,则mn= ;
(4)实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是边长为4cm的正方形
是边长为4cm的正方形 对角线的交点,
对角线的交点, 是
是 的中点,动点
的中点,动点 由点
由点 开始沿折线
开始沿折线 方向匀速运动,到点
方向匀速运动,到点 时停止运动,速度为
时停止运动,速度为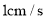 .设
.设 点的运动时间为
点的运动时间为 ,点
,点 的运动路径与
的运动路径与 、
、 所围成的图形面积为
所围成的图形面积为 ,则描述面积
,则描述面积 与时间
与时间 的关系的图象是( )
的关系的图象是( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的网格中,
 的三个顶点均在格点上,请按要求完成下列各题:
的三个顶点均在格点上,请按要求完成下列各题:
(1)画线段
 ,且使
,且使 ,连接
,连接 ;
;(2)线段
 的长为________,
的长为________, 的长为________,
的长为________,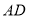 的长为________;
的长为________;(3)
 是________三角形,四边形
是________三角形,四边形 的面积是________;
的面积是________;(4)若点
 为
为 的中点,
的中点, 为
为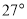 ,则
,则 的度数为________.
的度数为________.
相关试题

