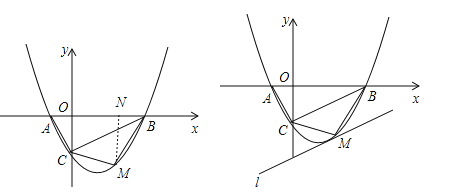
【题目】如图,抛物线![]() (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

参考答案:
【答案】(1)![]() ;(2)(
;(2)(![]() ,0);(3)4,M(2,﹣3).
,0);(3)4,M(2,﹣3).
【解析】试题分析:方法一:
(1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可.
(2)首先根据抛物线的解析式确定A点坐标,然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置,由此确定圆心坐标.
(3)△MBC的面积可由S△MBC=![]() BC×h表示,若要它的面积最大,需要使h取最大值,即点M到直线BC的距离最大,若设一条平行于BC的直线,那么当该直线与抛物线有且只有一个交点时,该交点就是点M.
BC×h表示,若要它的面积最大,需要使h取最大值,即点M到直线BC的距离最大,若设一条平行于BC的直线,那么当该直线与抛物线有且只有一个交点时,该交点就是点M.
方法二:
(1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可.
(2)通过求出A,B,C三点坐标,利用勾股定理或利用斜率垂直公式可求出AC⊥BC,从而求出圆心坐标.
(3)利用三角形面积公式,过M点作x轴垂线,水平底与铅垂高乘积的一半,得出△MBC的面积函数,从而求出M点.
试题解析:解:方法一:
(1)将B(4,0)代入抛物线的解析式中,得: 0=16a﹣![]() ×4﹣2,即:a=
×4﹣2,即:a=![]() ,∴抛物线的解析式为:
,∴抛物线的解析式为: ![]() .
.
(2)由(1)的函数解析式可求得:A(﹣1,0)、C(0,﹣2);
∴OA=1,OC=2,OB=4,即:OC2=OAOB,又:OC⊥AB,∴△OAC∽△OCB,得:∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,∴△ABC为直角三角形,AB为△ABC外接圆的直径;
所以该外接圆的圆心为AB的中点,且坐标为:(![]() ,0).
,0).
(3)已求得:B(4,0)、C(0,﹣2),可得直线BC的解析式为:y=![]() x﹣2;
x﹣2;
设直线l∥BC,则该直线的解析式可表示为:y=![]() x+b,当直线l与抛物线只有一个交点时,可列方程:
x+b,当直线l与抛物线只有一个交点时,可列方程:
![]() x+b=
x+b=![]() ,即:
,即: ![]() ,且△=0;
,且△=0;
∴4﹣4×![]() (﹣2﹣b)=0,即b=﹣4;
(﹣2﹣b)=0,即b=﹣4;
∴直线l:y=![]() x﹣4.
x﹣4.
所以点M即直线l和抛物线的唯一交点,有:  ,解得:
,解得: ![]()
即 M(2,﹣3).
过M点作MN⊥x轴于N,S△BMC=S梯形OCMN+S△MNB﹣S△OCB=![]() ×2×(2+3)+
×2×(2+3)+![]() ×2×3﹣
×2×3﹣![]() ×2×4=4.
×2×4=4.
方法二:
(1)将B(4,0)代入抛物线的解析式中,得: 0=16a﹣![]() ×4﹣2,即:a=
×4﹣2,即:a=![]() ,∴抛物线的解析式为:
,∴抛物线的解析式为: ![]() .
.
(2)∵y=![]() (x﹣4)(x+1),∴A(﹣1,0),B(4,0).C(0,﹣2),∴KAC=
(x﹣4)(x+1),∴A(﹣1,0),B(4,0).C(0,﹣2),∴KAC=![]() =﹣2,KBC=
=﹣2,KBC=![]() =
=![]() ,∴KAC×KBC=﹣1,∴AC⊥BC,∴△ABC是以AB为斜边的直角三角形,△ABC的外接圆的圆心是AB的中点,△ABC的外接圆的圆心坐标为(
,∴KAC×KBC=﹣1,∴AC⊥BC,∴△ABC是以AB为斜边的直角三角形,△ABC的外接圆的圆心是AB的中点,△ABC的外接圆的圆心坐标为(![]() ,0).
,0).
(3)过点M作x轴的垂线交BC′于H,∵B(4,0),C(0,﹣2),∴lBC:y=![]() x﹣2,设H(t,
x﹣2,设H(t, ![]() t﹣2),M(t,
t﹣2),M(t, ![]() ),∴S△MBC=
),∴S△MBC=![]() ×(HY﹣MY)(BX﹣CX)=
×(HY﹣MY)(BX﹣CX)=![]() ×(
×(![]() t﹣2﹣
t﹣2﹣![]() )(4﹣0)=﹣t2+4t,∴当t=2时,S有最大值4,∴M(2,﹣3).
)(4﹣0)=﹣t2+4t,∴当t=2时,S有最大值4,∴M(2,﹣3).

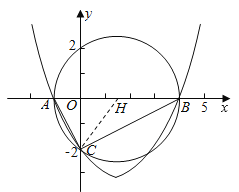
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”,这个三角形给出了(a+b)n (n=1,2,3,4,…)的展开式的系数规律(按n的次数由大到小的顺序):
1 1 (a+b)1=a+b
1 2 1 (a+b)2=a2+2ab+b2
1 3 3 1 (a+b)3=a3+3a2b+3ab2+b3
1 4 6 4 1 (a+b)4=a4+4a3b+6a2b2+4ab3+b4
…… ……
请依据上述规律,写出(x1)2019展开式中含x2018项的系数是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年是“精准扶贫”攻坚关键年,某扶贫工作队为对口扶贫村引进建立了一村集体企业,并无偿提供一笔无息贷款作为启动资金,双方约定:①企业生产出的产品全部由扶贫工作队及时联系商家收购;②企业从生产销售的利润中,要保证按时发放工人每月最低工资32000元.已知该企业生产的产品成本为20元/件,月生产量y(千件)与出厂价x(元)(25≤x≤50)的函数关系可用图中的线段AB和BC表示,其中AB的解析式为y=﹣
 x+m(m为常数).
x+m(m为常数).(1)求该企业月生产量y(千件)与出厂价x(元)之间的函数关系式,并写出自变量x的取值范围.
(2)当该企业生产出的产品出厂价定为多少元时,月利润W(元)最大?最大利润是多少?[月利润=(出厂价﹣成本)×月生产量﹣工人月最低工资].

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上。

(1)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(2)若连接AA′、BB′,则这两条线段之间的关系是________________;
(3)在图中画出△ABC的高CD;
(4)△A′B′C′的面积为________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A.
 B.
B.  C.
C.
 D.
D. 


-
科目: 来源: 题型:
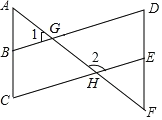
查看答案和解析>>【题目】如图,已知AF分别与BD、CE交于点G、H,其中∠1+∠2=180°.
(1)判断BD和CE有怎样的位置关系,并说明理由;
(2)若∠A=∠F,探索∠C与∠D的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).

(1)图2中的阴影部分的面积为 ;
(2)观察图2请你写出(a+b)2、(ab)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若m+n=5,mn=4,则mn= ;
(4)实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等 .
相关试题

