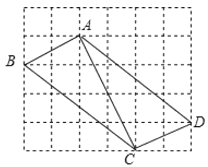
【题目】如图,在边长为1的小正方形组成的网格中,![]() 的三个顶点均在格点上,请按要求完成下列各题:
的三个顶点均在格点上,请按要求完成下列各题:

(1)画线段![]() ,且使
,且使![]() ,连接
,连接![]() ;
;
(2)线段![]() 的长为________,
的长为________,![]() 的长为________,
的长为________,![]() 的长为________;
的长为________;
(3)![]() 是________三角形,四边形
是________三角形,四边形![]() 的面积是________;
的面积是________;
(4)若点![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() ,则
,则![]() 的度数为________.
的度数为________.
参考答案:
【答案】(1)见解析;(2)![]() ,
,![]() ,5;(3)直角,10;(4)
,5;(3)直角,10;(4)![]()
【解析】
(1)根据题意,画出AD∥BC且使AD=BC,连接CD;
(2)在网格中利用直角三角形,先求AC ![]() 的值,再求出AC的长,CD的长,AD的长;
的值,再求出AC的长,CD的长,AD的长;
(3)利用勾股定理的逆定理判断直角三角形,再求出四边形ABCD的面积;
(4)把问题转化到Rt△ACB中,利用直角三角形斜边上的中线可知BE=AE=EC,根据等腰三角形性质即可解题.
(1)如图所示:AD、CD为所求作
(2)根据勾股定理得:![]()
故答案为:![]() ;
;![]() ;5
;5
(3)∵![]() ,
,![]()
∴![]()
∴![]() 是直角三角形,∠ACD=90°
是直角三角形,∠ACD=90°
∴四边形![]() 的面积是:
的面积是:![]()
故答案为:直角;10
(4)∵![]() ,
,![]()
∴四边形ABCD是平行四边形
∴AB//CD
∴∠BAC=∠ACD=90°
在Rt△ACD中,![]() 为
为![]() 的中点
的中点
∴AE=BE=CE, ∠ABC+∠ACB=90°
∴∠ACB=∠EAC=27°
∴∠ABC =63°
故答案为:![]()
-
科目: 来源: 题型:
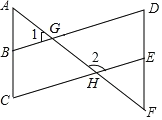
查看答案和解析>>【题目】如图,已知AF分别与BD、CE交于点G、H,其中∠1+∠2=180°.
(1)判断BD和CE有怎样的位置关系,并说明理由;
(2)若∠A=∠F,探索∠C与∠D的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).

(1)图2中的阴影部分的面积为 ;
(2)观察图2请你写出(a+b)2、(ab)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若m+n=5,mn=4,则mn= ;
(4)实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是边长为4cm的正方形
是边长为4cm的正方形 对角线的交点,
对角线的交点, 是
是 的中点,动点
的中点,动点 由点
由点 开始沿折线
开始沿折线 方向匀速运动,到点
方向匀速运动,到点 时停止运动,速度为
时停止运动,速度为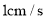 .设
.设 点的运动时间为
点的运动时间为 ,点
,点 的运动路径与
的运动路径与 、
、 所围成的图形面积为
所围成的图形面积为 ,则描述面积
,则描述面积 与时间
与时间 的关系的图象是( )
的关系的图象是( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(观察思考)
怎样判断两条直线是否平行?
如图①,很难看出直线a、n是否平行,可添加“第三条线”(截线c),把判断两条直线的位置关系转化为判断两个角的数量关系.我们称直线c为“辅助线”.在部分代数问题中,很难用算术直接计算出结果,于是,引入字母解决复杂问题,我们称引入的字母为“辅助元”.事实上,使用“辅助线”、“辅助元”等“辅助元素”可以更容易地解决问题.

(理解运用)
(1)计算
 这个算式直接计算很麻烦,请你引入合适的“辅助元”完成计算.
这个算式直接计算很麻烦,请你引入合适的“辅助元”完成计算.(拓展提高)
(2)若关于x,y的方程组
 的解是
的解是 ,则关于x、y的方程组
,则关于x、y的方程组 的解为 .
的解为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:

其次,对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示:
测试项目
测试成绩/分
甲
乙
丙
笔试
92
90
95
面试
85
95
80
图二是某同学根据上表绘制的一个不完全的条形图.
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
如图1,⊙O1和⊙O2外切于点C,AB是⊙O1和⊙O2外公切线,A、B为切点,
求证:AC⊥BC
证明:过点C作⊙O1和⊙O2的内公切线交AB于D,
∵DA、DC是⊙O1的切线
∴DA=DC.
∴∠DAC=∠DCA.
同理∠DCB=∠DBC.
又∵∠DAC+∠DCA+∠DCB+∠DBC=180°,
∴∠DCA+∠DCB=90°.
即AC⊥BC.
根据上述材料,解答下列问题:
(1)在以上的证明过程中使用了哪些定理?请写出两个定理的名称或内容;
(2)以AB所在直线为x轴,过点C且垂直于AB的直线为y轴建立直角坐标系(如图2),已知A、B两点的坐标为(﹣4,0),(1,0),求经过A、B、C三点的抛物线y=ax2+bx+c的函数解析式;
(3)根据(2)中所确定的抛物线,试判断这条抛物线的顶点是否落在两圆的连心O1O2上,并说明理由.


相关试题

