【题目】如图,已知四边形OABC是平行四边形,点A(2,2)和点C(6,0),连结CA并延长交y轴于点D.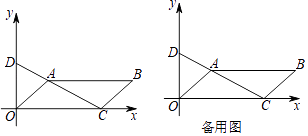
(1)求直线AC的函数解析式.
(2)若点P从点C出发以2个单位/秒沿x轴向左运动,同时点Q从点O出发以1个单位/秒沿x轴向右运动,过点P、Q分别作x轴垂线交直线CD和直线OA分别于点E、F,猜想四边形EPQF的形状(点P、Q重合除外),并证明你的结论.
(3)在(2)的条件下,当点P运动多少秒时,四边形EPQF是正方形?
参考答案:
【答案】
(1)解:设直线AC的解析式为y=kx+b,
∵点A(2,2)和点C(6,0),
∴ ![]() ,
,
∴ 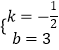 ,
,
∴直线AC的解析式为y=﹣ ![]() x+3
x+3
(2)解:如图1,
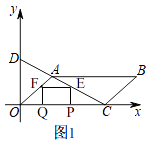
∵点A的坐标为(2,2),
∴直线OA的解析式为y=x,
∵点Q从点O出发以1个单位/秒沿x轴向右运动,
∴OQ=t,
∴F(t,t),
∴FQ=t,
∵点P从点C出发以2个单位/秒沿x轴向左运动,
∴CP=2t,
∴OP=6﹣2t,
由(1)知,直线AC的解析式为y=﹣ ![]() x+3,
x+3,
∴E(6﹣2t,t),
∴PE=t,
∴PE=FQ,
∵FQ⊥x轴,PE⊥x轴,
∴∠PQF=90°,FQ∥PE,
∵PE=FQ,
∴四边形PEFQ是平行四边形,
∵∠PQF=90°,
∴平行四边形PEFQ是矩形
(3)解:由(2)知,PC=2t,OQ=t,PE=t,
∴PQ=OC﹣OQ﹣CP=6﹣t﹣2t=6﹣3t,或PQ=OQ+CP﹣OC=3t﹣6,
∵四边形PEFQ是正方形,
∴PQ=PE,
∴6﹣3t=t或3t﹣6=t,
∴t= ![]() 或t=3,即:点P运动
或t=3,即:点P运动 ![]() 秒或3秒时,四边形EPQF是正方形
秒或3秒时,四边形EPQF是正方形
【解析】(1)利用待定系数法即可求出直线AC的解析式;(2)先利用待定系数法求出直线OA的解析式,进而求出点E,F坐标,即可得出PE=FQ,即可得出结论;(3)先分两种情况(点Q在点P左侧或右侧)求出PQ,利用PE=PQ建立方程即可求出时间.
【考点精析】关于本题考查的确定一次函数的表达式和正方形的判定方法,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“日啖荔枝三百颗,不辞长作岭南人”,广东的夏季盛产荔枝,桂味、糯米糍是荔枝的品种之一.佳佳同学先用52元购买2千克桂味和1千克糯米糍;几天后,他用76元购买1千克桂味和3千克糯米糍.(前后两次两种荔枝的售价不变)
(1)求桂味、糯米糍的售价分别是每千克多少元?
(2)若佳佳同学用y元买了这两种荔枝共中10千克,设买了x千克桂味. ①写出y与x的函数关系式.
②若要求糯米糍的重量不少于桂味重量的3倍,请帮佳佳同学设计一个购买方案,使所需的费用最少,并求出最少费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的一个外角为50°,则它的底角为_________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,BC=4,将△ADC沿AC折叠,点D落在点D′处,CD′与AB交于点F.
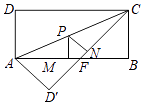
(1)求线段AF的长.
(2)求△AFC的面积.
(3)点P为线段AC(不含点A、C)上任意一点,PM⊥AB于点M,PN⊥CD′于点N,试求PM+PN的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:﹣2x3+18x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
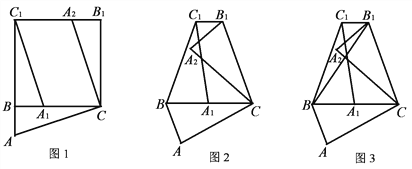
(1)如图1,在Rt△ABC中,∠ABC=90°,以点B为中心,把△ABC逆时针旋转90°,得到△A1BC1;再以点C为中心,把△ABC顺时针旋转90°,得到△A2B1C,连接C1B1,则C1B1与BC的位置关系为_______;
(2)如图2,当△ABC是锐角三角形,∠ABC=α(α≠60°)时,将△ABC按照(1)中的方式旋转α,连接C1B1,探究C1B1与BC的位置关系,写出你的探究结论,并加以证明;
(3)如图3,在图2的基础上,连接B1B,若C1B1=
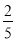 BC,△C1BB1的面积为4,则△B1BC的面积为 .
BC,△C1BB1的面积为4,则△B1BC的面积为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级(2)班40个学生某次数学测验成绩如下:
63,84,91,53,69,81,61,69,91,78,75,81,80,67,76,81,79,94,61,69,
89,70,70,87,81,86,90,88,85,67,71,82,87,75,87,95,53,65,74,77
数学老师按10分的组距分段,算出每个分数段学生成绩出现的频数,填入频数分页表:
(1)请把频数分布表、频数分布直方图补充完整并画出频数分布折线图;
(2)请你帮老师统计一下这次数学考试的及格率(60分以上含60分为及格)及优秀率(90分以上含90分为优秀);
(3)请说明哪个分数段的学生最多?哪个分数段的学生最少?


相关试题

