【题目】“日啖荔枝三百颗,不辞长作岭南人”,广东的夏季盛产荔枝,桂味、糯米糍是荔枝的品种之一.佳佳同学先用52元购买2千克桂味和1千克糯米糍;几天后,他用76元购买1千克桂味和3千克糯米糍.(前后两次两种荔枝的售价不变)
(1)求桂味、糯米糍的售价分别是每千克多少元?
(2)若佳佳同学用y元买了这两种荔枝共中10千克,设买了x千克桂味. ①写出y与x的函数关系式.
②若要求糯米糍的重量不少于桂味重量的3倍,请帮佳佳同学设计一个购买方案,使所需的费用最少,并求出最少费用.
参考答案:
【答案】
(1)解:设桂味的售价是每千克m元,糯米糍的售价是每千克n元,
根据题意得: ![]() ,
,
解得: ![]() .
.
答:桂味的售价是每千克16元,糯米糍的售价是每千克20元.
(2)解:①设买了x千克桂味,则买了(10﹣x)千克糯米糍,
根据题意得:y=16x+20(10﹣x)=﹣4x+200(0<x<10).
②∵糯米糍的重量不少于桂味重量的3倍,
∴10﹣x≥3x,
∴x≤ ![]() .
.
∵y=﹣4x+200中,k=﹣4<0,
∴y值随x值的增大而减小,
∴当x= ![]() 时,y取最小值,最小值为190.
时,y取最小值,最小值为190.
答:当购买桂味 ![]() 千克、糯米糍
千克、糯米糍 ![]() 千克时,所需的费用最少,最少费用为190元.
千克时,所需的费用最少,最少费用为190元.
【解析】(1)设桂味的售价是每千克m元,糯米糍的售价是每千克n元,根据“用52元购买2千克桂味和1千克糯米糍,用76元购买1千克桂味和3千克糯米糍”,即可得出关于m、n的二元一次方程组,解之即可得出结论;(2)①设买了x千克桂味,则买了(10﹣x)千克糯米糍,根据总价=单价×购买数量,即可得出y与x的函数关系式;②由糯米糍的重量不少于桂味重量的3倍可得出关于x的一元一次不等式,解之即可得出x的取值范围,再利用一次函数的性质即可解决最值问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=x3﹣2y3+3x2y+xy2﹣3xy+4,B=y3﹣x3﹣4x2y﹣3xy﹣3xy2+3,C=y3+x2y+2xy2+6xy﹣6,试说明对于x、y、z的任何值A+B+C是常数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3x+2)(3x﹣2)﹣5x(x﹣1)﹣(2x﹣1)2.
-
科目: 来源: 题型:
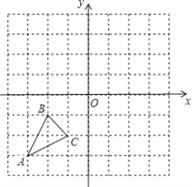
查看答案和解析>>【题目】如图,已知A(﹣3,﹣3),B(﹣2,﹣1),C(﹣1,﹣2)是直角坐标平面上三点.
(1)请画出△ABC关于原点O对称的△A1B1C1;
(2)请写出点B关于y轴对称的点B2的坐标,若将点B2向上平移h个单位,使其落在△A1B1C1内部,指出h的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的一个外角为50°,则它的底角为_________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,BC=4,将△ADC沿AC折叠,点D落在点D′处,CD′与AB交于点F.
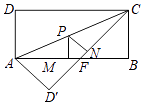
(1)求线段AF的长.
(2)求△AFC的面积.
(3)点P为线段AC(不含点A、C)上任意一点,PM⊥AB于点M,PN⊥CD′于点N,试求PM+PN的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形OABC是平行四边形,点A(2,2)和点C(6,0),连结CA并延长交y轴于点D.
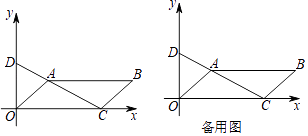
(1)求直线AC的函数解析式.
(2)若点P从点C出发以2个单位/秒沿x轴向左运动,同时点Q从点O出发以1个单位/秒沿x轴向右运动,过点P、Q分别作x轴垂线交直线CD和直线OA分别于点E、F,猜想四边形EPQF的形状(点P、Q重合除外),并证明你的结论.
(3)在(2)的条件下,当点P运动多少秒时,四边形EPQF是正方形?
相关试题

