【题目】如图,△ABC中,AB=AC,AD=BD=BC,则∠A的度数是( )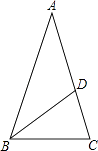
A.30°
B.36°
C.45°
D.20°
参考答案:
【答案】B
【解析】解:设∠A=x°.
∵BD=AD,
∴∠A=∠ABD=x°,(等边对等角)
∠BDC=∠A+∠ABD=2x°,(三角形的外角等于相邻两内角的和)
∵BD=BC,
∴∠BDC=∠BCD=2x°,(等边对等角)
∵AB=AC,
∴∠ABC=∠BCD=2x°,(等边对等角)
在△ABC中x+2x+2x=180,(三角形的内角和等于180°)
解得:x=36,
∴∠A=36°.
故答案为:B.
等腰三角形的性质1:等腰三角形的两个底角相等(简写“等边对等角”)
图中有多个与∠A有直接和间接关系的角,设其中∠A为未知量,代数思维解决几何问题。
-
科目: 来源: 题型:
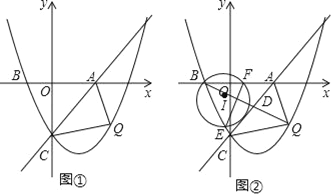
查看答案和解析>>【题目】如图,直线l:y=x﹣
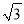 与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y=
与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y=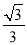 x2+bx+c经过点B(﹣1,0)和点C.
x2+bx+c经过点B(﹣1,0)和点C.(1)填空:直接写出抛物线的解析式:_____;
(2)已知点Q是抛物线y=
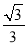 x2+bx+c在第四象限内的一个动点.
x2+bx+c在第四象限内的一个动点.①如图,连接AQ、CQ,设点Q的横坐标为t,△AQC的面积为S,求S与t的函数关系式,并求出S的最大值;
②连接BQ交AC于点D,连接BC,以BD为直径作⊙I,分别交BC、AB于点E、F,连接EF,求线段EF的最小值,并直接写出此时Q点的坐标.
-
科目: 来源: 题型:
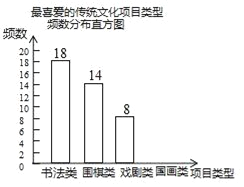
查看答案和解析>>【题目】某校为更好地培养学生兴趣,开展“拓展课程走班选课”活动,随机抽查了部分学生,了解他们最喜爱的项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表
项目类型
频数
频率
书法类
18
a
围棋类
14
0.28
喜剧类
8
0.16
国画类
b
0.20
根据以上信息完成下列问题:
(1)频数分布表中a=_____,b=_____;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc>0;②a﹣b+c<0;③2a+b﹣c<0;④4a+2b+c>0,⑤若点(﹣
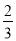 ,y1)和(
,y1)和(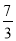 ,y2)在该图象上,则y1>y2.其中正确的结论是_____(填入正确结论的序号)
,y2)在该图象上,则y1>y2.其中正确的结论是_____(填入正确结论的序号)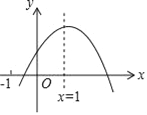
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两支球队的人数相等,平均身高都是1.72米,方差分别是S甲2=0.35,S乙2=0.27,则甲、乙两队中身高较整齐的是队.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必然是( )
A.菱形
B.对角线相互垂直的四边形
C.正方形
D.对角线相等的四边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】命题“有两边相等的三角形是等腰三角形”,它的逆命题是___________________________.
相关试题

