【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(﹣2, ![]() ),顶点坐标为N(﹣1,
),顶点坐标为N(﹣1, ![]() ),且与x轴交于A、B两点,与y轴交于C点.
),且与x轴交于A、B两点,与y轴交于C点.
(1)求抛物线的解析式;
(2)点P为抛物线对称轴上的动点,当△PBC为等腰三角形时,求点P的坐标;
(3)在直线AC上是否存在一点Q,使△QBM的周长最小?若存在,求出Q点坐标;若不存在,请说明理由.

参考答案:
【答案】(1)抛物线的解析式为y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ;(2)当△PBC为等腰三角形时,点P的坐标为(﹣1,
;(2)当△PBC为等腰三角形时,点P的坐标为(﹣1, ![]() ),(﹣1,
),(﹣1, ![]() ),(﹣1,2
),(﹣1,2![]() ),(﹣1,﹣2
),(﹣1,﹣2![]() ),(﹣1,0);(3)在直线AC上存在一点Q(﹣
),(﹣1,0);(3)在直线AC上存在一点Q(﹣![]() ,
, ![]() ),使△QBM的周长最小.
),使△QBM的周长最小.
【解析】分析:(1)先由抛物线的顶点坐标为N(﹣1, ![]() ),可设其解析式为y=a(x+1)2+
),可设其解析式为y=a(x+1)2+![]() ,再将M(﹣2,
,再将M(﹣2, ![]() )代入,得
)代入,得![]() =a(﹣2+1)2+
=a(﹣2+1)2+![]() ,解方程求出a的值即可得到抛物线的解析式;
,解方程求出a的值即可得到抛物线的解析式;
(2)先求出抛物线y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 与x轴交点A、B,与y轴交点C的坐标,再根据勾股定理得到BC=
与x轴交点A、B,与y轴交点C的坐标,再根据勾股定理得到BC=![]() =2
=2![]() .设P(﹣1,m),当△PBC为等腰三角形时分三种情况进行讨论:①CP=CB;②BP=BC;③PB=PC;
.设P(﹣1,m),当△PBC为等腰三角形时分三种情况进行讨论:①CP=CB;②BP=BC;③PB=PC;
(3)先由勾股定理的逆定理得出BC⊥AC,连结BC并延长至B′,使B′C=BC,连结B′M,交直线AC于点Q,由轴对称的性质可知此时△QBM的周长最小,由B(﹣3,0),C(0, ![]() ),根据中点坐标公式求出B′(3,2
),根据中点坐标公式求出B′(3,2![]() ),再运用待定系数法求出直线MB′的解析式为y=
),再运用待定系数法求出直线MB′的解析式为y=![]() x+
x+![]() ,直线AC的解析式为y=﹣
,直线AC的解析式为y=﹣![]() x+
x+![]() ,然后解方程组
,然后解方程组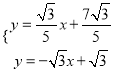 ,即可求出Q点的坐标.
,即可求出Q点的坐标.
本题解析:
(1)由抛物线顶点坐标为N(﹣1,![]() ),可设其解析式为y=a(x+1)2+
),可设其解析式为y=a(x+1)2+![]() ,
,
将M(﹣2,![]() )代入,得
)代入,得![]() =a(﹣2+1)2+
=a(﹣2+1)2+![]() ,
,
解得a=﹣![]() ,
,
故所求抛物线的解析式为y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ;
;
(2)∵y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() ,
,
∴x=0时,y=![]() ,
,
∴C(0,![]() ).
).
y=0时,﹣![]() x2﹣
x2﹣![]() x+
x+![]() =0,
=0,
解得x=1或x=﹣3,
∴A(1,0),B(﹣3,0),
∴BC=![]() =2
=2![]() .
.
设P(﹣1,m),
当CP=CB时,有CP=![]() =2
=2![]() ,解得m=
,解得m=![]() ±
±![]() ;
;
当BP=BC时,有BP=![]() =2
=2![]() ,解得m=±2
,解得m=±2![]() ;
;
当PB=PC时,![]() =
=![]() ,解得m=0,
,解得m=0,
综上,当△PBC为等腰三角形时,点P的坐标为(﹣1, ![]() ),(﹣1,
),(﹣1, ![]() ),(﹣1,2
),(﹣1,2![]() ),(﹣1,﹣2
),(﹣1,﹣2![]() ),(﹣1,0);
),(﹣1,0);
(3)由(2)知BC=2![]() ,AC=2,AB=4,
,AC=2,AB=4,
所以BC2+AC2=AB2,即BC⊥AC.
连结BC并延长至B′,使B′C=BC,连结B′M,交直线AC于点Q,
∵B、B′关于直线AC对称,
∴QB=QB′,
∴QB+QM=QB′+QM=MB′,
所以此时△QBM的周长最小.
由B(﹣3,0),C(0,![]() ),易得B′(3,2
),易得B′(3,2![]() ).
).
设直线MB′的解析式为y=kx+n,
将M(﹣2,![]() ),B′(3,2
),B′(3,2![]() )代入,
)代入,
得![]() ,解得
,解得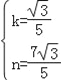 ,
,
即直线MB′的解析式为y=![]() x+
x+![]() .
.
同理可求得直线AC的解析式为y=﹣![]() x+
x+![]() .
.
由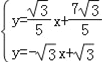 ,解得
,解得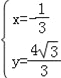 ,即Q(﹣
,即Q(﹣![]() ,
,![]() ).
).
所以在直线AC上存在一点Q(﹣![]() ,
, ![]() ),使△QBM的周长最小.
),使△QBM的周长最小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】圣母大学计算机系的史戈宇教授带一家人去旅行,途中汽车被劫走报警911,警察无作为,汽车上安装的MS系统,可以提示汽车与手机APP间的直线距离。史教授用“贪心算法”把被盗车辆位置确定在了图中灰色的区域里,这是一个以暴乱和枪击闻名的地区。当史教授开车从E向A的方向行驶时,汽车与手机APP间的直线距离逐渐变小,从A向F的方向行驶时,汽车与手机APP问的直线距离逐渐变大.当史教授开车从F向B的方向行驶时,汽车与手机APP间的直线距离逐渐变小,从B向G的方向行驶时,汽车与手机APP间的直线距离逐渐变大. 史教授再次报警后,警察根据史教授确定的被盗汽车的位置,很快找到了被盗汽车根据你学的数学知识,在图中,画出被盗汽车的位置.

-
科目: 来源: 题型:
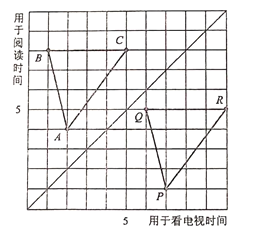
查看答案和解析>>【题目】图中,点A,B,C,P,Q,R显示了6名学生平均每周用于阅读课外书的时间和用于看电视的时间(单位:h)
(1)用有序数对表示图中点A,B,C,P,Q,R
(2)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(3)三角形ABC的图形经过怎样的变换后得到三角形PQR的图形?其中点A对应点P,点B对应点Q,点C对应点R
-
科目: 来源: 题型:
查看答案和解析>>【题目】张翔上午7:30出发,从学校骑自行车去县城,路程全长20km,中途因道路施工步行一段路.他步行的平均速度是5km/h
(1)若张翔骑车的平均速度是15km/h,当天上午9:00到达县城,则他骑车与步行各用多少时间?
(2)若张翔必须在当天上午9:00之前赶到县城,他的步行平均速度不变,则他骑车的平均速度应在什么范围内?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式:①
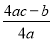 =-1;②ac+b+1=0;③abc>0;④a-b+c>0.正确的序号是______________.
=-1;②ac+b+1=0;③abc>0;④a-b+c>0.正确的序号是______________.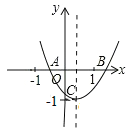
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价x元.据此规律,请回答:
(1)商场日销售量增加______件,每件商品盈利______.元(用含
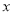 的代数式表示);
的代数式表示);(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到1428元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形
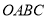 的顶点
的顶点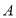 、
、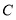 分别落在
分别落在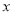 轴、
轴、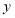 轴正半轴上,点
轴正半轴上,点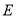 在边
在边 上,点
上,点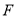 在边
在边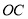 上,且
上,且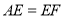 ,已知
,已知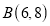 ,
,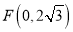 .
.(1)求点
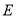 的坐标;
的坐标;(2)点
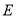 关于点
关于点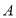 的对称点为点
的对称点为点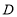 ,点
,点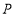 从
从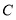 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线 运动,设
运动,设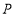 点的运动时间为
点的运动时间为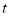 秒,
秒,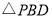 的面积为
的面积为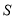 ,用含
,用含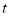 的代数式表示
的代数式表示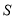 ;
;(3)在(2)的条件下,点
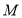 为平面内一点,点
为平面内一点,点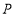 在线段
在线段 上运动时,作
上运动时,作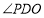 的平分线交
的平分线交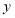 轴于点
轴于点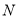 ,
,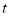 为何值时,四边形
为何值时,四边形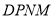 为矩形?并求此时点
为矩形?并求此时点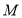 的坐标.
的坐标.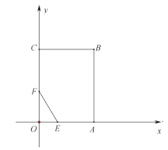
相关试题

