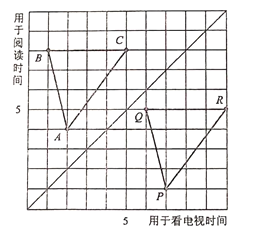
【题目】图中,点A,B,C,P,Q,R显示了6名学生平均每周用于阅读课外书的时间和用于看电视的时间(单位:h)
(1)用有序数对表示图中点A,B,C,P,Q,R
(2)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(3)三角形ABC的图形经过怎样的变换后得到三角形PQR的图形?其中点A对应点P,点B对应点Q,点C对应点R
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)根据图中点的位置写出坐标即可.
(2)图中方格纸的对角线的左上方的点表示阅读课外书的时间大于看电视的时间.
右下方的点表示阅读课外书的时间小于看电视的时间.
(3)根据平移规律解决问题即可.
解:(1)由题意得:A(2,4),B(1,8),C(5,8),P(7,1),Q(6,5),R(10,5).
(2)图中方格纸的对角线的左上方的点表示阅读课外书的时间大于看电视的时间,右下方的点表示阅读课外书的时间小于看电视的时间;
(3)三角形ABC的图形向右平移5个单位,再向下平移3个单位得到三角形PQR的图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,海中有一个小岛
 ,它的周围14海里内有暗礁,在小岛正西方有一点
,它的周围14海里内有暗礁,在小岛正西方有一点 测得在北偏东60°方向上有一灯塔
测得在北偏东60°方向上有一灯塔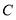 ,灯塔
,灯塔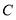 在小岛
在小岛 北偏东15°方向上20海里处,渔船跟踪鱼群沿
北偏东15°方向上20海里处,渔船跟踪鱼群沿 方向航行,每小时航行
方向航行,每小时航行 海里.
海里.(1)如果渔船不改变航向继续航行,有没有触礁危险?请说明理由.
(2)求渔船从
 点处航行到灯塔
点处航行到灯塔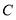 ,需要多少小时?
,需要多少小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,四边形ABCD是平行四边形,E,F是对角线AC上的两点,AE=CF.
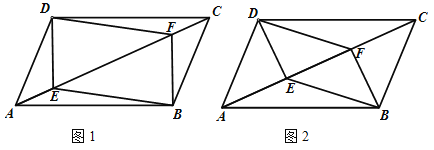
(1)求证:四边形DEBF是平行四边形;
(2)如果AE=EF=FC,请直接写出图中2所有面积等于四边形DEBF的面积的三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】圣母大学计算机系的史戈宇教授带一家人去旅行,途中汽车被劫走报警911,警察无作为,汽车上安装的MS系统,可以提示汽车与手机APP间的直线距离。史教授用“贪心算法”把被盗车辆位置确定在了图中灰色的区域里,这是一个以暴乱和枪击闻名的地区。当史教授开车从E向A的方向行驶时,汽车与手机APP间的直线距离逐渐变小,从A向F的方向行驶时,汽车与手机APP问的直线距离逐渐变大.当史教授开车从F向B的方向行驶时,汽车与手机APP间的直线距离逐渐变小,从B向G的方向行驶时,汽车与手机APP间的直线距离逐渐变大. 史教授再次报警后,警察根据史教授确定的被盗汽车的位置,很快找到了被盗汽车根据你学的数学知识,在图中,画出被盗汽车的位置.

-
科目: 来源: 题型:
查看答案和解析>>【题目】张翔上午7:30出发,从学校骑自行车去县城,路程全长20km,中途因道路施工步行一段路.他步行的平均速度是5km/h
(1)若张翔骑车的平均速度是15km/h,当天上午9:00到达县城,则他骑车与步行各用多少时间?
(2)若张翔必须在当天上午9:00之前赶到县城,他的步行平均速度不变,则他骑车的平均速度应在什么范围内?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(﹣2,
 ),顶点坐标为N(﹣1,
),顶点坐标为N(﹣1,  ),且与x轴交于A、B两点,与y轴交于C点.
),且与x轴交于A、B两点,与y轴交于C点.(1)求抛物线的解析式;
(2)点P为抛物线对称轴上的动点,当△PBC为等腰三角形时,求点P的坐标;
(3)在直线AC上是否存在一点Q,使△QBM的周长最小?若存在,求出Q点坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式:①
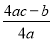 =-1;②ac+b+1=0;③abc>0;④a-b+c>0.正确的序号是______________.
=-1;②ac+b+1=0;③abc>0;④a-b+c>0.正确的序号是______________.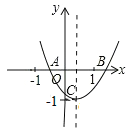
相关试题

