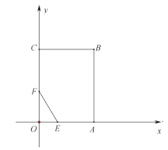
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别落在
分别落在![]() 轴、
轴、![]() 轴正半轴上,点
轴正半轴上,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() ,已知
,已知![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 关于点
关于点![]() 的对称点为点
的对称点为点![]() ,点
,点![]() 从
从![]() 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线![]() 运动,设
运动,设![]() 点的运动时间为
点的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() ;
;
(3)在(2)的条件下,点![]() 为平面内一点,点
为平面内一点,点![]() 在线段
在线段![]() 上运动时,作
上运动时,作![]() 的平分线交
的平分线交![]() 轴于点
轴于点![]() ,
,![]() 为何值时,四边形
为何值时,四边形![]() 为矩形?并求此时点
为矩形?并求此时点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
![]() ;(3)故当t=4时,四边形
;(3)故当t=4时,四边形![]() 为矩形,此时M(6,-3).
为矩形,此时M(6,-3).
【解析】
(1)先确定出点A的坐标,进而得出OA,最后在Rt△OEF中,利用勾股定理求出OE即可得出点E的坐标;
(2)分两种情况,用三角形的面积公式即可解决问题;
(3)先利用对称求出点D的坐标,进而得出OD,由角平分线的性质定理得出DP=OD求出点P的坐标,再利用勾股定理求出点N的坐标,根据矩形的性质,由点的平移方式即可求得点M的坐标.
解:(1)在矩形OABC中,B(6,8),
∴A(6,0),
∴OA=6,
设OE=a,
∴EF=AE=OA-OE=6-a,
∵![]() ,
,
![]() ,
,
在Rt△AEF中,根据勾股定理得,OE2+OF2=EF2,
∴a2+12=(6-a)2,
∴![]() ,
,
∴![]() ;
;
(2)∵BC∥OA,B(6,8),OC=AB=8,
∴P(t,8),PB=|t-6|
①当点P在边BC上时,如图1,
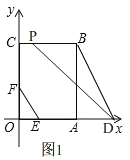
∴0≤t<6,
∴PB=6-t,
![]() ;
;
②当点P在CB的延长时,如图2,

∴t>6,
∴PB=t-6,
![]() ,
,
即:![]() ;
;
(3)由(1)知,![]() ,
,
∴![]() ,
,
∵点D是点E关于点A的对称点,
∴![]() ,
,
∴![]() ,
,
如图3,
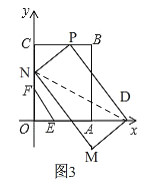
∵四边形DPNM是矩形,
∴∠DPN=90°=∠DON,
∴NP⊥DP,NO⊥OD,
∵DN是∠PDO的平分线,
∴NO=NP,
在Rt△NDO和Rt△NDP中,
![]() ,
,
∴Rt△NDO≌Rt△NDP(HL),
∴![]() ,
,
∵P(t,8),![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() (点P在线段BC上,舍去)
(点P在线段BC上,舍去)
∴P(4,8)
设N(0,n),
∴ON=n,
∴PN=n,CN=OC-ON=8-n,
在Rt△CNP中,根据勾股定理得,CN2+CP2=PN2,
∴(8-n)2+16=n2,
∴n=5,
∴N(0,5),
即点P(4,8)平移到N(0,5),向左平移四个单位,向下平移3个单位,
点D(10,0)由此方式平移后得到的M(6,-3).
故当t=4时,四边形![]() 为矩形,此时M(6,-3).
为矩形,此时M(6,-3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(﹣2,
 ),顶点坐标为N(﹣1,
),顶点坐标为N(﹣1,  ),且与x轴交于A、B两点,与y轴交于C点.
),且与x轴交于A、B两点,与y轴交于C点.(1)求抛物线的解析式;
(2)点P为抛物线对称轴上的动点,当△PBC为等腰三角形时,求点P的坐标;
(3)在直线AC上是否存在一点Q,使△QBM的周长最小?若存在,求出Q点坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式:①
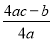 =-1;②ac+b+1=0;③abc>0;④a-b+c>0.正确的序号是______________.
=-1;②ac+b+1=0;③abc>0;④a-b+c>0.正确的序号是______________.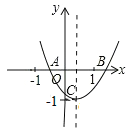
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价x元.据此规律,请回答:
(1)商场日销售量增加______件,每件商品盈利______.元(用含
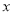 的代数式表示);
的代数式表示);(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到1428元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程:
(1)x2-7x+6=0; (2)(5x-1)2=3(5x-1);
(3)2x2-2x+3=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.

(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥(x-2)2+m的x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将
 沿
沿 翻折,点
翻折,点 的对称点是点
的对称点是点 ,
, ,
,(1)求证:四边形
 是菱形;
是菱形;(2)如图2,在
 上取一点
上取一点 ,连接
,连接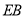 并延长至点
并延长至点 ,在
,在 上取一点
上取一点 ,连接
,连接 ,若
,若 ,求证:
,求证: .
.
相关试题

