【题目】商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价x元.据此规律,请回答:
(1)商场日销售量增加______件,每件商品盈利______.元(用含![]() 的代数式表示);
的代数式表示);
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到1428元?
参考答案:
【答案】(1)2x,50-x;(2)每件商品降价36元,商场日盈利可达1428元.
【解析】
(1)降价1元,可多售出2件,降价x元,可多售出2x件,每件盈利的钱数=原来的盈利-降低的钱数;
(2)等量关系为:每件商品的盈利×可卖出商品的件数=1428,把相关数值代入计算得到合适的解即可.
解:(1)降价1元,可多售出2件,降价x元,可多售出2x件,盈利的钱数=50-x,故答案为2x,50-x;
(2)由题意得:(50-x)(30+2x)=1428(0≤x<50)
化简得:x2-35x+300=0,即(x-15)(x-20)=0,
解得:x1=36,x2=-1(舍去),
答:每件商品降价36元,商场日盈利可达1428元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张翔上午7:30出发,从学校骑自行车去县城,路程全长20km,中途因道路施工步行一段路.他步行的平均速度是5km/h
(1)若张翔骑车的平均速度是15km/h,当天上午9:00到达县城,则他骑车与步行各用多少时间?
(2)若张翔必须在当天上午9:00之前赶到县城,他的步行平均速度不变,则他骑车的平均速度应在什么范围内?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(﹣2,
 ),顶点坐标为N(﹣1,
),顶点坐标为N(﹣1,  ),且与x轴交于A、B两点,与y轴交于C点.
),且与x轴交于A、B两点,与y轴交于C点.(1)求抛物线的解析式;
(2)点P为抛物线对称轴上的动点,当△PBC为等腰三角形时,求点P的坐标;
(3)在直线AC上是否存在一点Q,使△QBM的周长最小?若存在,求出Q点坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式:①
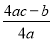 =-1;②ac+b+1=0;③abc>0;④a-b+c>0.正确的序号是______________.
=-1;②ac+b+1=0;③abc>0;④a-b+c>0.正确的序号是______________.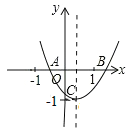
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形
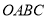 的顶点
的顶点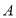 、
、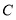 分别落在
分别落在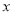 轴、
轴、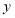 轴正半轴上,点
轴正半轴上,点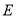 在边
在边 上,点
上,点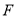 在边
在边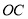 上,且
上,且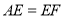 ,已知
,已知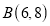 ,
,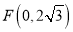 .
.(1)求点
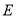 的坐标;
的坐标;(2)点
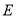 关于点
关于点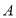 的对称点为点
的对称点为点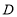 ,点
,点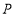 从
从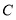 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线 运动,设
运动,设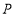 点的运动时间为
点的运动时间为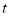 秒,
秒,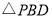 的面积为
的面积为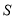 ,用含
,用含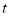 的代数式表示
的代数式表示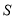 ;
;(3)在(2)的条件下,点
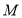 为平面内一点,点
为平面内一点,点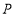 在线段
在线段 上运动时,作
上运动时,作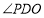 的平分线交
的平分线交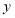 轴于点
轴于点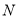 ,
,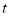 为何值时,四边形
为何值时,四边形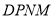 为矩形?并求此时点
为矩形?并求此时点 的坐标.
的坐标.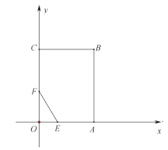
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程:
(1)x2-7x+6=0; (2)(5x-1)2=3(5x-1);
(3)2x2-2x+3=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.

(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥(x-2)2+m的x的取值范围.
相关试题

