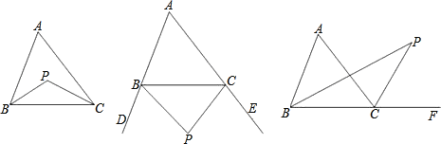
【题目】如图,△ABC中,∠A=40°,
(1)若点P是∠ABC与∠ACB平分线的交点,求∠P的度数;
(2)若点P是∠CBD与∠BCE平分线的交点,求∠P的度数;
(3)若点P是∠ABC与∠ACF平分线的交点,求∠P的度数;
(4)若∠A=β,求(1)(2)(3)中∠P的度数(用含β的代数式表示,直接写出结果)

参考答案:
【答案】(1)∠BPC=110°;(2)∠BPC =70°;(3)∠BPC=20°;(4)(1)中∠P=![]() β+90°;(2)中∠P=90°-
β+90°;(2)中∠P=90°-![]() β;(3)中∠P=
β;(3)中∠P=![]() β.
β.
【解析】
(1)由三角形内角和定理可知∠ABC+∠ACB的度数,根据点P是∠ABC与∠ACB平分线的交点,可知![]() 的度数,再次利用三角形内角和定理即可得出∠P度数;
的度数,再次利用三角形内角和定理即可得出∠P度数;
(2)由三角形的外角和定理可以得到![]() ∠DBC与
∠DBC与![]() ∠BCE关于∠A的关系,再利用三角形内角和定理即可求出答案;
∠BCE关于∠A的关系,再利用三角形内角和定理即可求出答案;
(3)由三角形的外角和定理和角平分线的定义可以得到∠P=![]() ,即可得出答案;
,即可得出答案;
(4)由(1)(2)(3)证明过程,容易得到答案.
(1)∵∠A=40°,
∴∠ABC+∠ACB=140°,
∴∠PBC+∠PCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×140°=70°,
×140°=70°,
∴∠BPC=180°-70°=110°;
(2)∵∠DBC=∠A+∠ACB,
∵P为△ABC两外角平分线的交点,
∴![]() ∠DBC=
∠DBC=![]() ∠A+
∠A+![]() ∠ACB,
∠ACB,
同理可得:![]() ∠BCE=
∠BCE=![]() ∠A+
∠A+![]() ∠ABC,
∠ABC,
∵∠A+∠ACB+∠ABC=180°,
∴![]() (∠ACB+∠ABC)=90°-
(∠ACB+∠ABC)=90°-![]() ∠A,
∠A,
∵180°-∠BPC=![]() ∠DBC+
∠DBC+![]() ∠BCE=
∠BCE=![]() ∠A+
∠A+![]() ∠ACB+
∠ACB+![]() ∠A+
∠A+![]() ∠ABC,
∠ABC,
∴180°-∠BPC=∠A+![]() ∠ACB+
∠ACB+![]() ∠ABC,180°-∠BPC=∠A+90°-
∠ABC,180°-∠BPC=∠A+90°-![]() ∠A,
∠A,
∴∠BPC=90°-![]() ∠A=70°;
∠A=70°;
(3)∵点P是∠ABC与∠ACF平分线的交点
∴![]()
∵∠PCF=∠P+∠PBC,∠ACF=∠A+∠ABC
∴2(∠P+∠PBC)=∠A+∠ABC
∴![]()
(4)若![]() 在(1)中
在(1)中![]() ;在(2)中,同理得
;在(2)中,同理得![]() ;在(3)中同理可得∠P=
;在(3)中同理可得∠P=![]() β.
β.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长方形ABCD中,AB=8cm,BC=12cm,E为AB的中点,动点P在线段BC上以4cm/s的速度由点B向C运动,同时,动点Q在线段CD上由点C向点D运动,设运动时间为t(s).

(1)当t=2时,求△EBP的面积;
(2)若动点Q以与动点P不同的速度运动,经过多少秒,△EBP与△CQP全等?此时点Q的速度是多少?
(3)若动点Q以(2)中的速度从点C出发,动点P以原来的速度从点B同时出发,都逆时针沿长方形ABCD的四边形运动,经过多少秒,点P与点Q第一次在长方形ABCD的哪条边上相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场将每件进价为80元的A商品按每件100元出售,一天可售出128件.经过市场调查,发现这种商品的销售单价每降低1元,其日销量可增加8件.设该商品每件降价x元,商场一天可通过A商品获利润y元.
(1)求y与x之间的函数解析式(不必写出自变量x的取值范围)
(2)A商品销售单价为多少时,该商场每天通过A商品所获的利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AD是△ABC的中线,AE⊥AB,AF⊥AC,且AE=AB,AF=AC,AD=3,AB=4.

(1)求AC长度的取值范围;
(2)求EF的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,A、B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.

(1)若|x+2y-10|+|2x-y|=0,试分别求出1秒钟后△AOB的面积;
(2)如图2,所示,设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,问:点A、B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由;
(3)如图3所示,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC、∠FCA、∠ABC的平分线相交于点G,过点G作BE的垂线,垂足为H,设∠AGH=α,∠BGC=β,试探究出α和β满足的数量关系并给出证明.
-
科目: 来源: 题型:
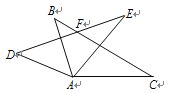
查看答案和解析>>【题目】如图,△ABC≌△ADE,BC与DE交于点F.若∠BAE=60°,∠DAC=160°,则∠DFC的度数为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组做“频率具有稳定性”的试验时,绘出某一结果出现的频率折线图如图所示,则符合这一结果的试验可能是( )

A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,掷出的点数是5
C.任意写一个整数,它能被2整除
D.从一个装有2个红球和1个白球的袋子中任取一球(这些球除颜色外完全相同),取到的是白球
相关试题

