【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.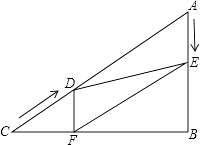
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出t的值,如果不能,说明理由;
(3)在运动过程中,四边形BEDF能否为正方形?若能,求出t的值;若不能,请说明理由.
参考答案:
【答案】
(1)
证明:∵RT△ABC中,∠B=90°,∠A=60°,
∴∠C=90°﹣∠A=30°.
又∵在RT△CDF中,∠C=30°,CD=4t
∴DF= ![]() CD=2t,
CD=2t,
∴DF=AE
(2)
解:∵DF∥AB,DF=AE,
∴四边形AEFD是平行四边形,
当AD=AE时,四边形AEFD是菱形,
即60﹣4t=2t,解得:t=10,
即当t=10时,四边形AEFD是菱形
(3)
解:四边形BEDF不能为正方形,理由如下:
当∠EDF=90°时,DE∥BC.
∴∠ADE=∠C=30°
∴AD=2AE
∵CD=4t,
∴DF=2t=AE,
∴AD=4t,
∴4t+4t=60,
∴t= ![]() 时,∠EDF=90°
时,∠EDF=90°
但BF≠DF,
∴四边形BEDF不可能为正方形
【解析】(1)由已知条件可得RT△CDF中∠C=30°,即可知DF= ![]() CD=AE=2t;(2)由(1)知DF∥AE且DF=AE,即四边形ADFE是平行四边形,若构成菱形,则邻边相等即AD=AE,可得关于t的方程,求解即可知;(3)四边形BEDF不为正方形,若该四边形是正方形即∠EDF=90°,即DE∥AB,此时AD=2AE=4t,根据AD+CD=AC求得t的值,继而可得DF≠BF,可得答案.
CD=AE=2t;(2)由(1)知DF∥AE且DF=AE,即四边形ADFE是平行四边形,若构成菱形,则邻边相等即AD=AE,可得关于t的方程,求解即可知;(3)四边形BEDF不为正方形,若该四边形是正方形即∠EDF=90°,即DE∥AB,此时AD=2AE=4t,根据AD+CD=AC求得t的值,继而可得DF≠BF,可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校去年在某商场购买甲、乙两种不同足球,购买甲种足球共花费2400元,购买乙种足球共花费1600元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)今年学校为编排“足球操”,决定再次购买甲、乙两种足球共50个.如果两种足球的单价没有改变,而此次购买甲、乙两种足球的总费用不超过3500元,那么这所学校最少可购买多少个甲种足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面上有6条直线,共有12个不同的交点,画出它们可能的位置关系(画三种图形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2﹣2a﹣3=0,求代数式(2a﹣1)2﹣2(a+1)(a﹣1)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
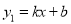 (k<0)与反比例函数
(k<0)与反比例函数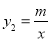 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1),B(n,2))
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1),B(n,2))(1)求反比例函数和一次函数的解析式;
(2)写出
 >
>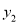 时,
时, 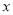 的取值范围;
的取值范围; 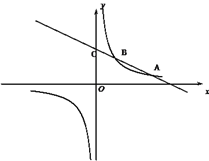
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,E为AD与CF的交点,AE=ED,已知△ABC的面积是1,△BEF的面积是
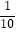 ,则△AEF的面积是;
,则△AEF的面积是;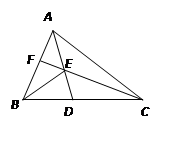
-
科目: 来源: 题型:
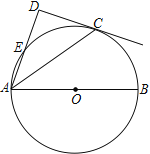
查看答案和解析>>【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O 于点E.
(1) 求证:AC平分∠DAB;
(2) 连接CE,若CE=6,AC=8,求AE的长.
相关试题

