【题目】某学校去年在某商场购买甲、乙两种不同足球,购买甲种足球共花费2400元,购买乙种足球共花费1600元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)今年学校为编排“足球操”,决定再次购买甲、乙两种足球共50个.如果两种足球的单价没有改变,而此次购买甲、乙两种足球的总费用不超过3500元,那么这所学校最少可购买多少个甲种足球?
参考答案:
【答案】(1) 购买一个甲种足球需60元,购买一个乙种足球需80元.(2) 这所学校此次最少可购买25个甲种足球.
【解析】试题分析:(1)设购买一个甲种足球需![]() 元,则购买一个乙种足球需(
元,则购买一个乙种足球需(![]() +20)元,然后根据两种球的购买数量之间的关系列方程即可求解;
+20)元,然后根据两种球的购买数量之间的关系列方程即可求解;
(2)根据购买两种球的价格不超过3500元,可列不等式求解.
试题解析:(1)设购买一个甲种足球需![]() 元,则购买一个乙种足球需(
元,则购买一个乙种足球需(![]() +20)元,
+20)元,
由题意得:
![]() .
.
解得: ![]() =60
=60
经检验, ![]() =60是原方程的解.
=60是原方程的解.
![]() +20=80
+20=80
答:购买一个甲种足球需60元,购买一个乙种足球需80元.
(2)设这所学校可购买![]() 个甲种足球,由题意得:
个甲种足球,由题意得:
![]() ≤3500,
≤3500,
解得: ![]() ≥25
≥25
答:这所学校此次最少可购买25个甲种足球.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知双曲线
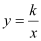 经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.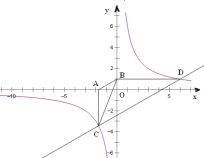
(1)求k的值;
(2)若△BCD的面积为12,求直线CD的解析式;
(3)判断AB与CD的位置关系,并说明理由.
-
科目: 来源: 题型:
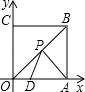
查看答案和解析>>【题目】如图,正方形OABC的边长为6,点A、C分别在x轴,y轴的正半轴上,点D(2,0)在OA上,P是OB上一动点,则PA+PD的最小值为 .
-
科目: 来源: 题型:
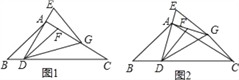
查看答案和解析>>【题目】在△ABC中,∠B=45°,∠C=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,在AG上取点F,连接DF.延长DA至E,使AE=AF,连接EG,DG,且GE=DF.
(1)若AB=2
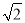 ,求BC的长;
,求BC的长;(2)如图1,当点G在AC上时,求证:BD=
 CG;
CG;(3)如图2,当点G在AC的垂直平分线上时,直接写出
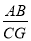 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面上有6条直线,共有12个不同的交点,画出它们可能的位置关系(画三种图形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2﹣2a﹣3=0,求代数式(2a﹣1)2﹣2(a+1)(a﹣1)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
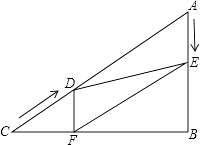
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出t的值,如果不能,说明理由;
(3)在运动过程中,四边形BEDF能否为正方形?若能,求出t的值;若不能,请说明理由.
相关试题

