【题目】如图,△ABC中,E为AD与CF的交点,AE=ED,已知△ABC的面积是1,△BEF的面积是 ![]() ,则△AEF的面积是;
,则△AEF的面积是;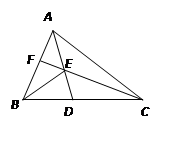
参考答案:
【答案】![]()
【解析】解:作AM⊥BC于M,EN⊥BC于N,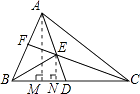
则EN∥AM,ED:AD=EN:AM,
∵AE=ED,
∴AD=2AE,
∴AM=2EN,
作AM⊥BC于M,EN⊥BC于N,得出EN∥AM,
∴S△ABC= ![]() BCAM,S△EBC=
BCAM,S△EBC= ![]() BCEN,
BCEN,
∴S△EBC= ![]() S△ABC又∵S△BEF=
S△ABC又∵S△BEF= ![]()
∴S△FBC=S△EBC+S△BEF= ![]() +
+ ![]() =
= ![]()
∴S△AFC=S△ABC-S△FBC=1- ![]() =
= ![]()
分别将AF和BF看做S△AFC和S△FBC的底,由于两个三角形的高相同,
∴AF:FB=S△AFC:S△FBC= ![]() :
: ![]() =2:3
=2:3
,
分别将AF和BF看做S△AFE和S△FBE的底,由于两个三角形的高相同
∴S△AFE:S△BEF=AF:FB=2:3,
∴S△AFE= ![]() ×
× ![]() =
= ![]()
根据平行线分线段成比例及线段中点的定义证得AM=2EN,可得到△EBC的面积等于△ABC面积的一半,再根据S△FBC=S△EBC+S△BEF及△ABC的面积是1,△BEF的面积是 ![]() , 求出△FBC的面积,再根据S△AFC=S△ABC-S△FBC , 就可求出△AFC的面积,然后根据S△AFC和S△FBC两个三角形的高相同,求出底边之比,根据S△AFE:S△BEF=AF:FB=2:3,即可求出答案。
, 求出△FBC的面积,再根据S△AFC=S△ABC-S△FBC , 就可求出△AFC的面积,然后根据S△AFC和S△FBC两个三角形的高相同,求出底边之比,根据S△AFE:S△BEF=AF:FB=2:3,即可求出答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2﹣2a﹣3=0,求代数式(2a﹣1)2﹣2(a+1)(a﹣1)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
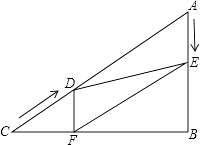
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出t的值,如果不能,说明理由;
(3)在运动过程中,四边形BEDF能否为正方形?若能,求出t的值;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
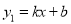 (k<0)与反比例函数
(k<0)与反比例函数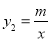 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1),B(n,2))
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1),B(n,2))(1)求反比例函数和一次函数的解析式;
(2)写出
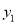 >
>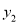 时,
时, 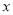 的取值范围;
的取值范围; 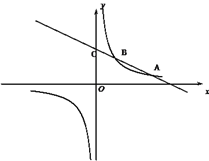
-
科目: 来源: 题型:
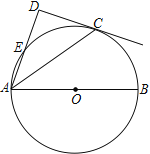
查看答案和解析>>【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O 于点E.
(1) 求证:AC平分∠DAB;
(2) 连接CE,若CE=6,AC=8,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】16的算术平方根和25平方根的和是( )
A. 9 B. -1 C. 9或-1 D. -9或1
-
科目: 来源: 题型:
查看答案和解析>>【题目】陈老师给42名学生每人买了一件纪念品,其中有:每支12元的钢笔,每把4元的圆规,每册16元的词典,共用了216元,则陈老师买了钢笔支,词典册;
相关试题

