【题目】如图.已知曲线是由顶点为T的二次函数 ![]() 的图象旋转45度得到,直线AB:
的图象旋转45度得到,直线AB: ![]() 交曲线于C,D两点.
交曲线于C,D两点.
(1)线段AT长为,
(2)在y轴上有一点P,且PC+PD 为最小,则点P的坐标为
参考答案:
【答案】
(1)![]()
(2)(0. ![]() )
)
【解析】解(1)依题可得:旋转前T点坐标为(0,1),
∵已知曲线是由顶点为T的二次函数 y =![]() x 2 + 1 的图象旋转45度得到,
x 2 + 1 的图象旋转45度得到,
∴OP=OT=1,
∴T(![]() ,
,![]() ),
),
又∵直线AB: x =![]() 交曲线于C,D两点,
交曲线于C,D两点,
∴A(![]() ,0),
,0),
∴AT=![]() =
=![]() .
.
所以答案是:![]() .
.
(2)求出D点关于y=-x的对称点,设对称点D‘(x',y')
可列式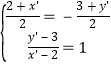
解得:D‘(-3,-2)
过C、D'画出直线,由C、D'的坐标求出函数关系。设y=kx+b![]()
解得:![]()
过CD’的直线为y=-11x-35
直线y=-11x-35与直线y=-x的交点即为P点
两式联立得:x=![]() ,y=
,y=![]()
可求出OP的长度为OP=![]() =
=![]()
所以P点在原坐标系中的坐标为(0,![]() )
)
【考点精析】根据题目的已知条件,利用二次函数的性质和旋转的性质的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面直角坐标系中,直线
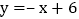 与直线
与直线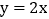 交与点
交与点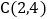 .
.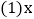 轴上是否存在点P,使
轴上是否存在点P,使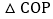 的面积是
的面积是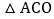 面积的二倍?若存在,直接写出点P的坐标;若不存在,说明理由.
面积的二倍?若存在,直接写出点P的坐标;若不存在,说明理由.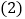 如图2,若点E是x轴上的一个动点,点E的横坐标为
如图2,若点E是x轴上的一个动点,点E的横坐标为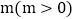 ,过点E作直线
,过点E作直线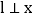 轴于点E,交直线
轴于点E,交直线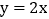 于点F,交直线
于点F,交直线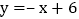 于点G,求m为何值时,
于点G,求m为何值时,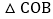 ≌
≌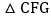 ?请说明理由.
?请说明理由. 在
在 的前提条件下,直线l上是否存在点Q,使
的前提条件下,直线l上是否存在点Q,使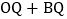 的值最小?若存在,直接写出点Q的坐标;若不存在,说明理由.
的值最小?若存在,直接写出点Q的坐标;若不存在,说明理由.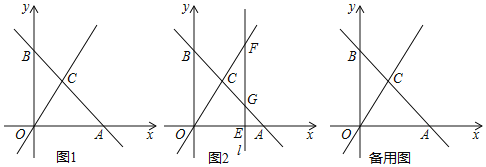
-
科目: 来源: 题型:
查看答案和解析>>【题目】汽车油箱中的余油量
 (升
(升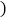 是它行驶的时间
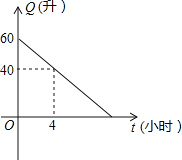
是它行驶的时间 (小 时) 的一次函数 . 某天该汽车外出时, 油箱中余油量与行驶时间的变化关系如图:
(小 时) 的一次函数 . 某天该汽车外出时, 油箱中余油量与行驶时间的变化关系如图:(1) 根据图象, 求油箱中的余油
 与行驶时间
与行驶时间 的函数关系 .
的函数关系 .(2) 从开始算起, 如果汽车每小时行驶 40 千米, 当油箱中余油 20 升时, 该汽车行驶了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:
① ∠AOE=65°;② OF平分∠BOD;③ ∠GOE=∠DOF;④ ∠AOE=∠GOD,其中正确结论的个数是( )

A. 4个B. 3个C. 2个D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.请将过程填写完整.

解:∵∠1=∠3,
又∠2=∠3(_______),
∴∠1=____,
∴______∥______(_______),
又∵CD∥EF,
∴AB∥_____,
∴∠1=∠4(两直线平行,同位角相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:
(1)计算: ( -2)0+|2﹣
-2)0+|2﹣ |+2sin60° ;
|+2sin60° ;
(2) 解分式方程:
解分式方程:  =
= -2
-2 -
科目: 来源: 题型:
查看答案和解析>>【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B、C两人中的某一人,以后的每一次传球都是由上次的接球者将球随机地传给其他两人中的某一人.(画出树状图或列表)
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
相关试题

