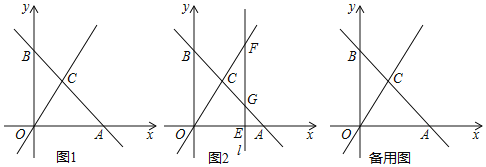
【题目】如图1,平面直角坐标系中,直线![]() 与直线
与直线![]() 交与点
交与点![]() .
.
![]() 轴上是否存在点P,使
轴上是否存在点P,使![]() 的面积是
的面积是![]() 面积的二倍?若存在,直接写出点P的坐标;若不存在,说明理由.
面积的二倍?若存在,直接写出点P的坐标;若不存在,说明理由.
![]() 如图2,若点E是x轴上的一个动点,点E的横坐标为
如图2,若点E是x轴上的一个动点,点E的横坐标为![]() ,过点E作直线
,过点E作直线![]() 轴于点E,交直线
轴于点E,交直线![]() 于点F,交直线
于点F,交直线![]() 于点G,求m为何值时,
于点G,求m为何值时,![]() ≌
≌![]() ?请说明理由.
?请说明理由.
![]() 在
在![]() 的前提条件下,直线l上是否存在点Q,使
的前提条件下,直线l上是否存在点Q,使![]() 的值最小?若存在,直接写出点Q的坐标;若不存在,说明理由.
的值最小?若存在,直接写出点Q的坐标;若不存在,说明理由.
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
![]() 利用一次函数图象上点的坐标特征可求出点A的坐标,由
利用一次函数图象上点的坐标特征可求出点A的坐标,由![]() 和
和![]() 等高且
等高且![]() 的面积是
的面积是![]() 面积的二倍,可得出
面积的二倍,可得出![]() ,进而可得出点P的坐标;
,进而可得出点P的坐标;
![]() 由
由![]() 可得出
可得出![]() ∽
∽![]() ,利用一次函数图象上点的坐标特征可求出点B的坐标,若要
,利用一次函数图象上点的坐标特征可求出点B的坐标,若要![]() ≌
≌![]() ,只需
,只需![]() ,即点C为线段BG的中点,结合点B,C的坐标可得出点G的坐标,再由
,即点C为线段BG的中点,结合点B,C的坐标可得出点G的坐标,再由![]() 轴可得出m的值;
轴可得出m的值;
![]() 作点O关于直线l对称的对称点D,连接BD,交直线l于点Q,此时
作点O关于直线l对称的对称点D,连接BD,交直线l于点Q,此时![]() 的值最小,由点O的坐标及直线l的解析式可得出点D的坐标,由点B,D的坐标,利用待定系数法求出直线BD的解析式,再利用一次函数图象上点的坐标特征即可求出点Q的坐标.
的值最小,由点O的坐标及直线l的解析式可得出点D的坐标,由点B,D的坐标,利用待定系数法求出直线BD的解析式,再利用一次函数图象上点的坐标特征即可求出点Q的坐标.
解:![]() 当
当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() 点A的坐标为
点A的坐标为![]() ,
,![]() .
.![]() 和
和![]() 等高,且
等高,且![]() 的面积是
的面积是![]() 面积的二倍,
面积的二倍,![]() ,
,![]() 点P的坐标为
点P的坐标为![]() 或
或![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() ∽
∽![]() .
.
当![]() 时,
时,![]() ,
,![]() 点B的坐标为
点B的坐标为![]() .
.
若要![]() ≌
≌![]() ,只需
,只需![]() .
.![]() 点B的坐标为
点B的坐标为![]() ,点C的坐标为
,点C的坐标为![]() ,
,![]() 点G的坐标为
点G的坐标为![]() .
.
又![]() 轴,
轴,![]() .
.![]() 当
当![]() 时,
时,![]() ≌
≌![]() .
.![]() 由
由![]() 可知,直线l的解析式为
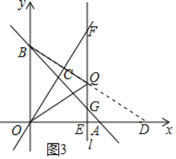
可知,直线l的解析式为![]() ,作点O关于直线l对称的对称点D,连接BD,交直线l于点Q,如图3所示.
,作点O关于直线l对称的对称点D,连接BD,交直线l于点Q,如图3所示.
![]() 点O,D关于直线l对称,
点O,D关于直线l对称,![]() ,点D的坐标为
,点D的坐标为![]() .
.![]() ,Q,D共线,
,Q,D共线,![]() 此时
此时![]() 取得最小值.
取得最小值.
设直线BD的解析式为![]() ,
,
将![]() ,
,![]() 代入
代入![]() ,得:
,得:![]() ,
,
解得: ,
,![]() 直线BD的解析式为
直线BD的解析式为![]() .
.
当![]() 时,
时,![]() ,
,![]() 直线l上存在点Q,使
直线l上存在点Q,使![]() 的值最小,点Q的坐标为
的值最小,点Q的坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 特例研究:如图
特例研究:如图 ,等边
,等边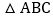 的边长为8,求等边
的边长为8,求等边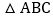 的高.
的高. 经验提升:
经验提升:如图
 ,在
,在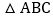 中,
中,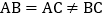 ,点P为射线BC上的任一点,过点P作
,点P为射线BC上的任一点,过点P作 ,
,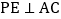 ,垂足分别为D、E,过点C作
,垂足分别为D、E,过点C作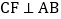 ,垂足为
,垂足为 补全图形,判断线段PD,PE,CF的数量关系,并说明理由.
补全图形,判断线段PD,PE,CF的数量关系,并说明理由.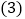 综合应用:
综合应用:如图
 ,在平面直角坐标系中有两条直线
,在平面直角坐标系中有两条直线 :
: ,
,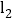 :
: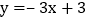 ,若线段BC上有一点M到
,若线段BC上有一点M到 的距离是1,请运用
的距离是1,请运用 中的结论求出点M的坐标.
中的结论求出点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的内心在y轴上,点C的坐标为(2,0),点B的坐标为(0,2),直线AC的解析式为: y=
 x1 ,则tanA的值是 .
x1 ,则tanA的值是 . 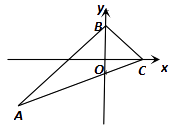
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边
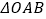 的边
的边 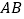 与
与 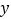 轴交于点
轴交于点 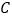 ,点
,点 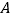 是反比例函数
是反比例函数 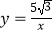
 图像上一点,若
图像上一点,若 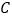 为
为 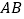 边的三等分点时,则等边
边的三等分点时,则等边 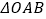 的边长为 .
的边长为 . 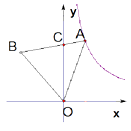
-
科目: 来源: 题型:
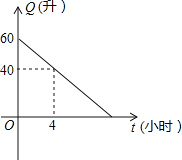
查看答案和解析>>【题目】汽车油箱中的余油量
 (升
(升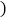 是它行驶的时间
是它行驶的时间 (小 时) 的一次函数 . 某天该汽车外出时, 油箱中余油量与行驶时间的变化关系如图:
(小 时) 的一次函数 . 某天该汽车外出时, 油箱中余油量与行驶时间的变化关系如图:(1) 根据图象, 求油箱中的余油
 与行驶时间
与行驶时间 的函数关系 .
的函数关系 .(2) 从开始算起, 如果汽车每小时行驶 40 千米, 当油箱中余油 20 升时, 该汽车行驶了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:
① ∠AOE=65°;② OF平分∠BOD;③ ∠GOE=∠DOF;④ ∠AOE=∠GOD,其中正确结论的个数是( )

A. 4个B. 3个C. 2个D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.已知曲线是由顶点为T的二次函数
 的图象旋转45度得到,直线AB:
的图象旋转45度得到,直线AB:  交曲线于C,D两点.
交曲线于C,D两点.
(1)线段AT长为,
(2)在y轴上有一点P,且PC+PD 为最小,则点P的坐标为
相关试题

