Question

【题目】A、B、C三人玩篮球传球游戏，游戏规则是:第一次传球由A将球随机地传给B、C两人中的某一人,以后的每一次传球都是由上次的接球者将球随机地传给其他两人中的某一人.(画出树状图或列表)
（1）求两次传球后，球恰在B手中的概率；
（2）求三次传球后，球恰在A手中的概率.

Answer 1

【答案】
（1）解：依题可画树状图如下：

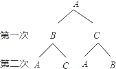
∵共有4种等可能的结果，两次传球后，球恰在B手中的只有1种情况，
∴两次传球后，球恰在B手中的概率为： .

（2）解：根据题意画树状图得：

∵共有8种等可能的结果，三次传球后，球恰在A手中的有2种情况，

∴三次传球后，球恰在A手中的概率为： ．

【解析】（1）根据题意可画出树状图，从而得出共有4种等可能的结果；两次传球后球恰在B手中的只有1种情况，根据概率公式即可求出两次传球后，球恰在B手中的概率 .
（2）根据题意可画出树状图，从而得出共有8种等可能的结果；三次传球后，球恰在A手中的有2种情况，根据概率公式即可求出三次传球后，球恰在A手中的概率.
【考点精析】本题主要考查了列表法与树状图法和概率公式的相关知识点，需要掌握当一次试验要设计三个或更多的因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法求概率；一般地，如果在一次试验中，有n种可能的结果，并且它们发生的可能性都相等，事件A包含其中的m中结果，那么事件A发生的概率为P（A）=m/n才能正确解答此题．