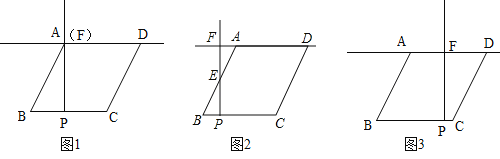
【题目】如图,在菱形ABCD中,AB=10,∠ABC=60°.点P从点B沿BC以每秒1个单位长的速度匀速运动,射线PF随点P移动,始终保持与BC垂直,并交折线BA﹣AC于点E,交直线AD于点F.设点P运动时间为t秒,且点P只在BC上运动.
(1)当t为何值时,BP=AF?
(2)设直线PF扫过菱形ABCD的面积为S,试用t的式子表示S.(写解题过程)



参考答案:
【答案】(1)当t为![]() 秒时,BP=AF;(2)①当0≤t≤5时,S=
秒时,BP=AF;(2)①当0≤t≤5时,S=![]() t2,
t2,
②当5<t≤10时,S=5![]() t﹣
t﹣![]() .
.
【解析】试题分析:(1)当E是AB的中点时,AF=BP,根据PF⊥BC,∠ABC=60°,可求解.
(2)当0≤t≤5时,扫过的是三角形的面积,以后扫过的是四边形的面积,根据面积公式可求出函数式.
试题解析:解:(1)∵PF⊥BC,∠ABC=60°,AB=10,∴sin60°=![]() ,PF=5
,PF=5![]() ,当E为PF的中点时,BP=AF,∴PE=
,当E为PF的中点时,BP=AF,∴PE=![]() PF=
PF=![]() ,∴BP=
,∴BP=![]() ,由题意得:PB=t,∴t=
,由题意得:PB=t,∴t=![]() ,则当t为
,则当t为![]() 秒时,BP=AF;
秒时,BP=AF;
(2)由题意得:PB=t,PE=![]() t.
t.
当F与A重合时,如图1.∵∠BAP=30°,AB=10,∴PB=5,∴t=5.
分两种情况:
①当0≤t≤5时,S=S△BPE=![]() PBPE=
PBPE=![]() ×
×![]() =
=![]() t2.
t2.
②当5<t≤10时,扫过的图形是梯形,AF=PB﹣5=t﹣5,S=S梯形ABPF=![]() PF(AF+PB)=
PF(AF+PB)=![]() ×
×![]() (t﹣5+t)5=5
(t﹣5+t)5=5![]() t﹣
t﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△AOB中点O是原点,点A在y轴上,点B的坐标是(2
 ,2),小明做一个数学实验,在x轴上取一动点C,以AC为一边画出等边△ACP,移动点C时,探究点P的位置变化情况.
,2),小明做一个数学实验,在x轴上取一动点C,以AC为一边画出等边△ACP,移动点C时,探究点P的位置变化情况.
(1)如图,小明将点C移至x轴负半轴,在AC的右侧画出等边△ACP,并使得顶点P在第三象限时,连接BP,求证:△AOC≌△ABP;
(2)小明在x轴上移动点C,并在AC的右侧画出等边△ACP时,发现点P在某函数图象上,请求出点P所在函数图象的解析式.
(3)小明在x轴上移动点C点时,若在AC的左侧画出等边△ACP,点P会不会在某函数图象上?若会在某函数图象上,请直接写出该函数图象的解析式,若不在某函数图象上,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】自学下面材料后,解答问题
分母中含有未知数的不等式叫做分式不等式,如:
 ;
; 等
等 那么如何求出它们的解集呢?
那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负
 其字母表达式为:
其字母表达式为: 若
若 ,
, ,则
,则 ;若
;若 ,
, ,则
,则
 若
若 ,
, ,则
,则 ;若
;若 ,
, ,则
,则
反之:
 若
若 ,则
,则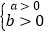 或
或
 若
若 ,则______或______.
,则______或______.根据上述规律
 求不等式
求不等式 的解集.
的解集. 直接写出一个解集为
直接写出一个解集为 或
或 的最简分式不等式.
的最简分式不等式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=120°,CE∥BD,DE∥AC,若AD=4,则四边形CODE的周长 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,规定把一个点先绕原点逆时针旋转45°,再作出它关于原点的对称点称为一次变换,已知点A的坐标为(﹣2,0),把点A经过连续2014次这样的变换得到的点A2014的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D,E分别是
 的边BC上两点,请你在下列三个式子
的边BC上两点,请你在下列三个式子 ,
, ,
, 中,选两个作为条件,余下的一个作为结论,编写一个说理题,并进行解答.
中,选两个作为条件,余下的一个作为结论,编写一个说理题,并进行解答.如图,已知点D,E分别是
 的边BC上两点______,______,那么______吗?为什么?
的边BC上两点______,______,那么______吗?为什么?
相关试题

