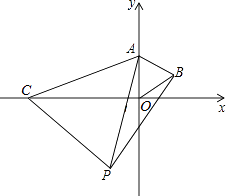
【题目】如图,等边△AOB中点O是原点,点A在y轴上,点B的坐标是(2 ![]() ,2),小明做一个数学实验,在x轴上取一动点C,以AC为一边画出等边△ACP,移动点C时,探究点P的位置变化情况.
,2),小明做一个数学实验,在x轴上取一动点C,以AC为一边画出等边△ACP,移动点C时,探究点P的位置变化情况.
(1)如图,小明将点C移至x轴负半轴,在AC的右侧画出等边△ACP,并使得顶点P在第三象限时,连接BP,求证:△AOC≌△ABP;
(2)小明在x轴上移动点C,并在AC的右侧画出等边△ACP时,发现点P在某函数图象上,请求出点P所在函数图象的解析式.
(3)小明在x轴上移动点C点时,若在AC的左侧画出等边△ACP,点P会不会在某函数图象上?若会在某函数图象上,请直接写出该函数图象的解析式,若不在某函数图象上,请说明理由.
参考答案:
【答案】
(1)
证明:如图,
∵△AOB与△ACP都是等边三角形,
∴OA=AB,A=AP,CAP=∠OAB=60°.
∴∠CAP+∠PAO=∠OAB+∠PAO.
∴∠CAO=∠PAB.
在△AOC与△PAB中,
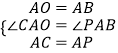 ,
,
∴△AOC≌△ABP
(2)
解:由(1)可知,△AOC≌△ABP,
∴∠COA=∠PBA=90°,
∴点P在过点A且与AB垂直的直线上,
在等边△AOB中,B(2 ![]() ,2),
,2),
∴AB=4,
当点C移动,使得P在y轴上时,
∵△PAB是直角三角形,∠PAB=60°,
∴PA= ![]() =8,
=8,
∴P(0,﹣4),
设直线PB的解析式为y=kx﹣4,把B(2 ![]() ,2)代入得到k=
,2)代入得到k= ![]() ,
,
∴点P所在函数图象的解析式为y= ![]() x﹣4
x﹣4
(3)
会在函数的图象上,如图作B的对称点B′,连接AB′,OB′.
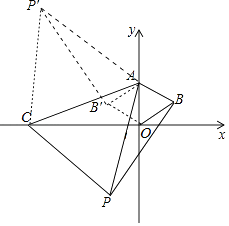
由(2)可知,P′B′⊥AB′,同法可得直线P′B′的解析式为t=﹣ ![]() x﹣4.
x﹣4.
∴该函数图象的解析式为y=﹣ ![]() x﹣4
x﹣4
【解析】(1)利用等边三角形的性质,根据SAS根据解决问题.(2)首先证明点P在过点A且与AB垂直的直线上,求出特殊点(P在y轴上的点),利用待定系数法即可解决问题.(3)如图作B的对称点B′,连接AB′,OB′.由(2)可知,P′B′⊥AB′,同法可得直线P′B′的解析式为t=﹣ ![]() x﹣4.
x﹣4.
【考点精析】通过灵活运用等边三角形的性质,掌握等边三角形的三个角都相等并且每个角都是60°即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为加强学生的体育锻炼,曾两次在某商场购买足球和篮球
 第一次购买6个足球和5个篮球共花费700元;第二次购买3个足球和7个篮球共花费710元.
第一次购买6个足球和5个篮球共花费700元;第二次购买3个足球和7个篮球共花费710元. 求足球和篮球的标价;
求足球和篮球的标价; 如果现在商场均以标价的6折对足球和篮球进行促销,学校决定从该商场再一次性购买足球和篮球60个,且总费用不能超过2500元,那么最多可以购买多少个篮球?
如果现在商场均以标价的6折对足球和篮球进行促销,学校决定从该商场再一次性购买足球和篮球60个,且总费用不能超过2500元,那么最多可以购买多少个篮球? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是_____,
证明你的结论.
(2)当四边形ABCD的对角线满足_____条件时,四边形EFGH是矩形;
(3)当四边形ABCD的对角线满足_____条件时,四边形EFGH是菱形;
(4)你学过的哪种特殊四边形的中点四边形是矩形?_____;
(5)你学过的哪种特殊四边形的中点四边形是菱形?_____;
(6)你学过的哪种特殊四边形的中点四边形是正方形?_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,经过的点A(﹣4,0)、点B(6,0)的 抛物线与y轴相交于点C(0,m),连接BC.

(1)若△OAC∽△OCB,请求出m的值;
(2)当m=3时,试求出抛物线的解析式;
(3)在(2)的条件下,若P为抛物线上位于x轴上方的一动点,以P、A、B、C为顶点的四边形面积记作S,当S取何值时,相应的点P有且只有3个? -
科目: 来源: 题型:
查看答案和解析>>【题目】自学下面材料后,解答问题
分母中含有未知数的不等式叫做分式不等式,如:
 ;
; 等
等 那么如何求出它们的解集呢?
那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负
 其字母表达式为:
其字母表达式为: 若
若 ,
, ,则
,则 ;若
;若 ,
, ,则
,则
 若
若 ,
, ,则
,则 ;若
;若 ,
, ,则
,则
反之:
 若
若 ,则
,则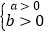 或
或
 若
若 ,则______或______.
,则______或______.根据上述规律
 求不等式
求不等式 的解集.
的解集. 直接写出一个解集为
直接写出一个解集为 或
或 的最简分式不等式.
的最简分式不等式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=10,∠ABC=60°.点P从点B沿BC以每秒1个单位长的速度匀速运动,射线PF随点P移动,始终保持与BC垂直,并交折线BA﹣AC于点E,交直线AD于点F.设点P运动时间为t秒,且点P只在BC上运动.
(1)当t为何值时,BP=AF?
(2)设直线PF扫过菱形ABCD的面积为S,试用t的式子表示S.(写解题过程)



相关试题

