【题目】综合题。
(1)如图,在方格纸中先通过________,由图形A得到图形B,再由图形B先________(怎样平移),再________(怎样旋转)得到图形C(对于平移变换要求回答出平移的方向和平移的距离;对于旋转变换要求回答出旋转中心、旋转方向和旋转角度);
(2)如图,如果点P、P3的坐标分别为(0,0)、(2,1),写出点P2的坐标是________;
(3)图形B能绕某点Q顺时针旋转90°得到图形C,则点Q的坐标是________;
(4)图形A能绕某点R顺时针旋转90°得到图形C,则点R的坐标是________; 注:方格纸中的小正方形的边长为1个单位长度.

参考答案:
【答案】(1)向上平移4个单位长;向右平移4个单位长度;绕点P2顺时针旋转90°;(2)(4,4);(3)(2,2);(4)(4,0).
【解析】试题分析:(1)如图,根据方格纸中A和B的位置可以确定图形变换方式;然后根据B和C也可以确定图形变换方式;
(2)根据(1)和已知条件首先确定P、P3和P2的关系,然后就可以确定P2的坐标;
(3)由于图形B能绕某点Q顺时针旋转90°得到图形C,首先可以确定两组旋转对应点,然后根据旋转的性质即可确定旋转中心Q的坐标;
(4)由于图形A能绕某点R顺时针旋转90°得到图形C,首先可以确定两组旋转对应点的坐标,然后根据旋转的性质即可确定点R的坐标.
试题解析:(1)根据题意可知,向上平移4个单位长度图形A得到图形B,图形B向右平移4个单位长度,再绕点P2顺时针旋转90°得到图形C.
故答案为:向上平移4个单位长,向右平移4个单位长度,绕点P2顺时针旋转90°.
(2)根据题意建立如图坐标系,根据图象可知P2(4,4).
故答案为:(4,4).
(3)观察图形可知旋转中心Q(2,2).
故答案为:(2,2).
(4)观察图形可知旋转中心R(4,0).
故答案为:(4,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
(1)如图1,在半对角四边形ABCD中,∠B=
 ∠D,∠C=
∠D,∠C= ∠A,求∠B与∠C的度数之和;
∠A,求∠B与∠C的度数之和;
(2)如图2,锐角△ABC内接于⊙O,若边AB上存在一点D,使得BD=BO.∠OBA的平分线交OA于点E,连结DE并延长交AC于点F,∠AFE=2∠EAF.

求证:四边形DBCF是半对角四边形;
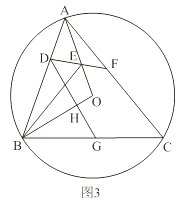
(3)如图3,在(2)的条件下,过点D作DG⊥OB于点H,交BC于点G.当DH=BG时,求△BGH与△ABC的面积之比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生体育活动的情况,学校设计了“你最喜欢的体育活动是哪一项(仅限一项)”的调查问卷.该校对学生进行随机抽样调查,以下是根据调查数据得到的不完整的统计图.请根据统计图中信息解答以下问题:
(1)该校对多少名学生进行了抽样调查?
(2)①请补全图1并标上数据,
②图2中x=__________% ;
(3)若该校共有学生900人,请你估计该校最喜欢跳绳项目的学生约有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,则∠A为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=36°,∠C=76°,AD、AF分别是△ABC的角平分线和高,求∠DAF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P在以AB为直径的半圆内,连接AP、BP,并延长分别交半圆于点C、D,连接AD、BC并延长交于点F,作直线PF,下列说法一定正确的是( )
①AC垂直平分BF;②AC平分∠BAF;③FP⊥AB;④BD⊥AF.

A. ①③ B. ①④ C. ②④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某城市规定用水收费标准如下:每户每月用水量不超过6米3时,水费按a元/米3收费;每户每月用水量超过6米3时,不超过的部分每立方米仍按a元收费,超过的部分按c元/米3收费,该市某用户今年3、4月份的用水量和水费如下表所示:
月份
用水量(m3)
收费(元)
3
5
7.5
4
9
27
(1)求a、c的值,并写出每月用水量不超过6米3和超过6米3时,水费与用水量之间的关系式;
(2)已知某户5月份的用水量为8米3,求该用户5月份的水费.
相关试题

