【题目】某校需购买一批课桌椅供学生使用,已知A型课桌椅230元/套,B型课桌椅200元/套.
(1)该校购买了A,B型课桌椅共250套,付款53000元,求A,B型课桌椅各买了多少套?
(2)因学生人数增加,该校需再购买100套A,B型课桌椅,现只有资金22000元,最多能购买A型课桌椅多少套?
参考答案:
【答案】
(1)解:设购买A型桌椅x套,B型桌椅y套,
依题意得: ![]() ,
,
解得 ![]() .
.
答:购买A型桌椅100套,B型桌椅150套
(2)解:设能购买A型课桌椅a套,
依题意得:230a+200(100﹣a)≤22000,
解得a≤ ![]() .
.
∵a是正整数,
∴a最大=66.
答:最多能购买A型课桌椅66套
【解析】(1)设购买A型桌椅x套,B型桌椅y套,根据“A,B型课桌椅共250套”、“A型课桌椅230元/套,B型课桌椅200元/套,付款53000元,”列出方程组并解答(2)设能购买A型课桌椅a套,则根据“最多能购买A型课桌椅多少套”列出不等式并解答即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=
 (k≠0)的图象交于A(﹣3,2),B(2,n).
(k≠0)的图象交于A(﹣3,2),B(2,n). 
(1)求反比例函数y= 的解析式;
的解析式;
(2)求一次函数y=ax+b的解析式;
(3)观察图象,直接写出不等式ax+b< 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,在正
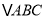 的内部,作
的内部,作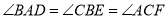 ,
, 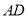 ,
, 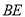 ,
, 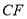 两两相交于
两两相交于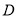 ,
, 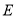 ,
, 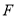 三点 (
三点 (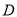 ,
, 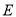 ,
, 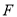 三点不重合).
三点不重合).(
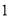 )
)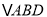 ,
,  ,
, 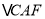 是否全等?如果是,请选择其中一对进行证明.
是否全等?如果是,请选择其中一对进行证明.(
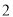 )
)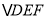 是否为正三角形?请说明理由.
是否为正三角形?请说明理由.(
 )进一步探究发现,
)进一步探究发现,  的三边存在一定的等量关系,设
的三边存在一定的等量关系,设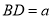 ,
, 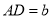 ,
, 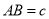 ,请探索
,请探索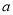 ,
, 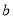 ,
, 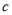 满足的等量关系.
满足的等量关系.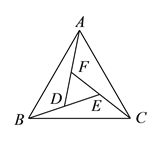
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级学生在学习《数据的分析》后,进行了检测,现将该校八(1)班学生的成绩统计如下表,并绘制成条形统计图(不完整).

分数(分)
人数(人)
68
4
78
7
80
3
88
5
90
10
96
6
100
5
(1)补全条形统计图;
(2)该班学生成绩的平均数为86.85分,写出该班学生成绩的中位数和众数;
(3)该校八年级共有学生500名,估计有多少学生的成绩在96分以上(含96分)?
(4)小明的成绩为88分,他的成绩如何,为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为
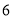 的正三角形纸片
的正三角形纸片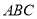 按如下顺序进行两次折叠,展开后,得折痕
按如下顺序进行两次折叠,展开后,得折痕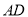 ,
,  (如图①),点
(如图①),点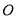 为其交点.
为其交点.(
 )探求
)探求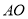 到
到 的数量关系,并说明理由.
的数量关系,并说明理由.(
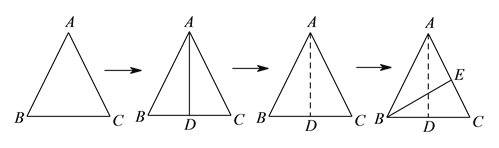
 )如图②,若
)如图②,若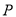 ,
, 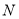 分别为
分别为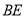 ,
, 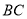 上的动点.
上的动点.①当
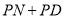 的长度取得最小值时,求
的长度取得最小值时,求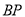 的长度.
的长度.②如图③,若点
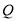 在线段
在线段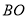 上,
上, 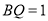 ,则
,则 的最小值
的最小值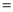 __________.
__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题: 学习了二次根式后,你会发现一些含有根号的式子可以写成另一个式子的平方,如3+2
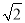 =(1+
=(1+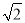 )2, 我们来进行以下的探索:
)2, 我们来进行以下的探索:设a+b
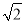 =(m+n
=(m+n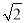 )2(其中a,b,m,n都是正整数),则有a+b
)2(其中a,b,m,n都是正整数),则有a+b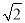 =m2+2n2+2mn
=m2+2n2+2mn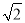 ,∴a=m+2n2 , b=2mn, 这样就得出了把类似a+b
,∴a=m+2n2 , b=2mn, 这样就得出了把类似a+b 的式子化为平方式的方法.
的式子化为平方式的方法.请仿照上述方法探索并解决下列问题:
(1)当a,b,m,n都为正整数时,若a﹣b
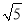 =(m﹣n
=(m﹣n )2 , 用含m,n的式子分别表示a,b,得a=________,b=________;
)2 , 用含m,n的式子分别表示a,b,得a=________,b=________; (2)利用上述方法,找一组正整数a,b,m,n填空:___﹣_____
 =(____﹣_____
=(____﹣_____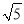 )2
)2 (3)a﹣4
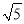 =(m﹣n
=(m﹣n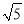 )2且a,m,n都为正整数,求a的值.
)2且a,m,n都为正整数,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点A(0,2)和点B(-a,3),且点B在正比例函数y=-3x的图象上.
(1)求a的值;
(2)求一次函数的解析式并画出它的图象;
(3)若P(m,y1),Q(m-1,y2)是这个一次函数图象上的两点,试比较y1与y2的大小.
相关试题

