搜索
【题目】如图，四边形
中，点
到直线
，
的距离相等为
， 
，
平分
，长为n，且
，四边形的面积为6．
（1）求线段的长；
（2）
为
延长线上一点，
，交
延长线于
，探究
、
、
的数量关系并说明理由；
（3）作
平行交
延长线于
，
平分
，反向延长线交延长线于
，若设
，
，试求
的值．
参考答案：
【答案】（1）1；（2）
，理由见解析；（3）
【解析】
分别以
、
所在的直线为x、
轴建立平面直角坐标系．
（1）利用二次根式的性质求出
、n的值，求出
、
两点坐标，由
，推出
，求出即可；
（2）如图2中，结论：．根据三角形内角和定理，三角形的外角的性质即可解决问题；
（3）由
，推出
，由
平分
，推出
，由
，推出
，由
平分
，可得
，由此即可解决问题．
解：分别以、所在的直线为x、轴建立平面直角坐标系．
（1）由题意
，
解得
，
，
，
．
如图1中，
，
，
．
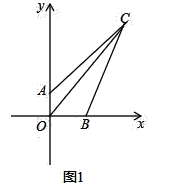
（2）如图2中，结论：．理由如下：
，
，
，
，
，
．
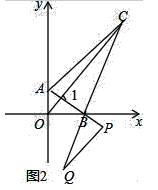
（3）如图3中，
，
，
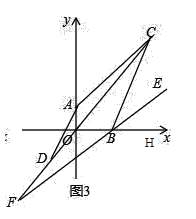
平分
，
，
，
，
，
平分，
，
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为
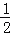．（1）试求袋中蓝球的个数；
（2）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表格法，求两次摸到都是白球的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线
与
轴相交于O、A两点（其中O为坐标原点），过点P（2，2a）作直线PM⊥x轴于点M，交抛物线于点B，点B关于抛物线对称轴的对称点为C（其中B、C不重合），连接AP交y轴于点N，连接BC和PC．
（1）
时，求抛物线的解析式和BC的长；（2）如图
时，若AP⊥PC，求
的值；（3）是否存在实数
，使
，若存在，求出的值；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，A，P，B，C是圆上的四个点，∠APC=∠CPB=60°，AP，CB的延长线相交于点D．
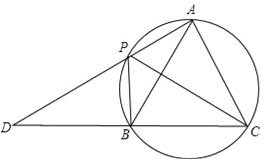
（1）求证：△ABC是等边三角形；
（2）若∠PAC=90°，AB=
，求PD的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图是常见的安全标记，其中是轴对称图形的是（ ）
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，平行四边形ABCD和平行四边形CDEF有公共边CD，边AB和EF在同一条直线上，AC⊥CD且AC=AF，过点A作AH⊥BC交CF于点G，交BC于点H，连接EG．
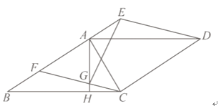
（1）若AE=2，CD=5，则△BCF的面积为 ；△BCF的周长为 ；
（2）求证：BC=AG+EG．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点(点D不与B、C重合)．以AD为边作正方形ADEF，连接CF．
（1）如图1，当点D在线段BC上时，请直接写出线段BD与CF的数量关系： ；
（2）如图2，当点D在线段BC的延长线上时，其它条件不变，若AC=2，CD=1，则CF= ；
（3）如图3，当点D在线段BC的反向延长线上时，且点A、F分别在直线BC的两侧，其它条件不变：
①请直接写出CF、BC、CD三条线段之间的关系： ；
②若连接正方形对角线AE、DF，交点为O，连接OC，探究△AOC的形状，并说明理由．
相关试题
