【题目】如图所示,平行四边形ABCD和平行四边形CDEF有公共边CD,边AB和EF在同一条直线上,AC⊥CD且AC=AF,过点A作AH⊥BC交CF于点G,交BC于点H,连接EG.
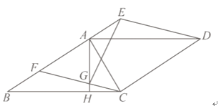
(1)若AE=2,CD=5,则△BCF的面积为 ;△BCF的周长为 ;
(2)求证:BC=AG+EG.
参考答案:
【答案】(1)3,![]() ;(2)见解析
;(2)见解析
【解析】
(1)根据平行和垂直的特点求出BF,AF,再根据勾股定理求出CD,根据FP与BA的比值求出面积,再根据勾股定理求CF,BC即可得到周长.
(2)在AD上截取AM=AG,连接CM,证△FAG≌△CAM;证△EFG≌△DCM.
解:(1)面积为3;周长为![]()
∵四边形ABCD和四边形CDEF都是平行四边形,
∴EF=CD,AB=CD,AB∥CD
∴EF=AB=CD=5
∴AE=EF-AE=5-2=3
∴BF=5-3=2
过F作FP⊥BC
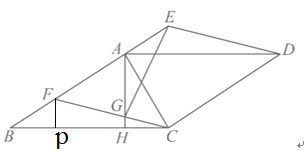
则FP:AH=BF:AB=2:5,
∴![]() ,
,
∵AC⊥CD,AB∥CD,
∴AB⊥AC,即∠BAC=90°,
∵AC=AF=3,
∴CF=![]() ,BC=
,BC=![]() ,
,
∴![]()
∴△BCF的面积为3,△BCF周长为![]()
(2)在AD上截取AM=AG,连接CM,
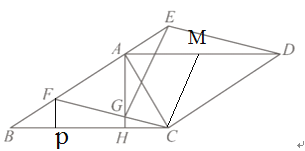
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC
∵AH⊥BC
∴AD⊥AH
∴∠DAH=90°
∵∠BAC=90°
∴∠DAH=∠BAC
∴∠DAH-∠CAH =∠BAC-∠CAH
∴∠BAH=∠CAD
∵AF=AC
∴△FAG≌△CAM
∴FG=CM,∠ACM=∠AFG
∵四边形CDEF是平行四边形,
∴EF∥CD,EF=CD,
∴∠DCF+∠AFC=180°,
∵AF=AC, ∠BAC=90°,
∴∠AFC=∠ACF=45°,
∴∠DCF=180°-∠AFC=135°,
∴∠ACM=∠AFG=45°,
∴∠DCM=∠FCD-∠ACF-∠ACM=45°,
∴∠AFG=∠DCM,
∴△EFG≌△DCM,
∴EG=DM,
∵AD=AM+DM,
∴AD=AG+EG,
∵AD=BC,
∴BC=AG+EG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.
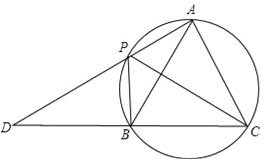
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=
 ,求PD的长.
,求PD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
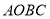 中,点
中,点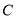 到直线
到直线 ,
,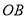 的距离相等为
的距离相等为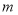 ,
, 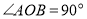 ,
,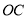 平分
平分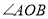 ,
,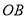 长为n,且
长为n,且 ,四边形
,四边形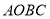 的面积为6.
的面积为6.
(1)求线段
 的长;
的长;(2)
 为
为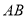 延长线上一点,
延长线上一点,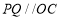 ,交
,交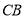 延长线于
延长线于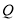 ,探究
,探究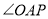 、
、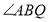 、
、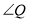 的数量关系并说明理由;
的数量关系并说明理由;(3)作
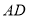 平行
平行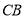 交
交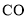 延长线于
延长线于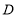 ,
,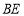 平分
平分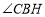 ,
,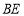 反向延长线交
反向延长线交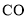 延长线于
延长线于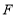 ,若设
,若设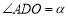 ,
,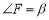 ,试求
,试求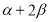 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是常见的安全标记,其中是轴对称图形的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时,请直接写出线段BD与CF的数量关系: ;
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,若AC=2,CD=1,则CF= ;
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:
①请直接写出CF、BC、CD三条线段之间的关系: ;
②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】母亲节过后,某校在本校学生中做了一次抽样调查,并把调查的结果分成三种类型:A. 不知道那一天是母亲节的;B. 知道但没有行动的;C. 知道并问候母亲的。如图是根据调查结果绘制的统计图(部分)。

(1)已知A类学生占被调查学生人数的
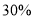 ,则被调查的学生共有多少人?
,则被调查的学生共有多少人?(2)计算B类学生的人数并根据计算结果补全统计图;
(3)如果该校共有学生2000人,你估计这个学校学生中有多少人知道母亲节并问候了母亲。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲。如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10 x元(x为整数)。
(1)(2分)直接写出每天游客居住的房间数量y与x的函数关系式。
(2)(4分)设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
(3)(4分)某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人。问:这天宾馆入住的游客人数最少有多少人?
相关试题

