【题目】(1)如图1已知:∠B=25°,∠BED=80°,∠D=55°.探究AB与CD有怎样的位置关系.
(2)如图2已知AB∥EF,试猜想∠B,∠F,∠BCF之间的关系,写出这种关系,并加以证明.
(3)如图3已知AB∥CD,试猜想∠1,∠2,∠3,∠4,∠5之间的关系,请直接写出这种关系,不用证明.



参考答案:
【答案】(1)详见解析(2)∠BCF=∠B+∠F(3)∠1+∠3+∠5=∠2+∠4
【解析】
(1)过点E作EF∥AB,得∠BEF =25°,得∠DEF=55°,从而可证AB∥CD;
(2)作CD∥AB,根据平行线的传递性得CD∥EF,则根据平行线的性质得∠BCD=∠B,∠DCF=∠F,所以∠BCD+∠DCF=∠B+∠F,故可得结论;
(3)方法同(2)
(1)过点E作EF∥AB

∵∠B=25°
∴∠BEF=∠B=25°
∵∠BED=80°
∴∠DEF=∠BED-∠BEF=55°
∵∠D=55°
∴∠D=∠DEF
∴EF∥CD
∴AB∥CD
(2)过点C作CD∥AB,则CD∥EF,

∵AB∥CD,
∴∠BCD=∠B,
∵CD∥EF,
∴∠DCF=∠F,
∴∠BCD+∠DCF=∠B+∠F,
即∠C=∠B+∠F.
(3)∠1+∠3+∠5=∠2+∠4,
如图,
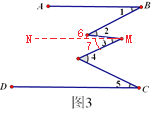
作MN∥AB,
由(2)的结论得到∠2=∠1+∠6,∠4=∠5+∠7,
∴∠2+∠4=∠1+∠6+∠5+∠7=∠1+∠3+∠5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=
 cm,OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒
cm,OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒 cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.(1)用t的式子表示△OPQ的面积S;
(2)求证:四边形OPBQ的面积是一个定值,并求出这个定值;
(3)当△OPQ与△PAB和△QPB相似时,抛物线y=
 x 2+bx+c经过B、P两点,过线段BP上一动点M作y轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.
x 2+bx+c经过B、P两点,过线段BP上一动点M作y轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长为1个单位长度,建立如图所示的平面直角坐标系,△ABC的顶点均为格点,把△ABC向右平移5个单位长度得到△A1B1C1,再作出△ABC关于x轴对称的△A2B2C2.
(1)在图中画出△A1B1C1和△A2B2C2;
(2)点
 在
在 轴上,且△ABP与△ABC的面积相等,则点P坐标为______;
轴上,且△ABP与△ABC的面积相等,则点P坐标为______;(3)横、纵坐标均为整数的点为整数点,在第二象限中的整数点M满足OM<OC,直接写出整数点
 的所有可能坐标.
的所有可能坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在平面直角坐标系中,作出下列各点,A(-3,4), B(-3,-2),O(0,0),并把各点连起来.
(2)画出△ABO先向下平移2个单位,再向右平移4 个单位得到的图形△A1B1o1,并直接写出A1坐标
(3) 直接写出三角形ABO的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(-1,0),B(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC.(提示:平行四边形的面积=底×高)
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)
 的值是否发生变化,若不变请求出该值,若会变请并请说明理由.
的值是否发生变化,若不变请求出该值,若会变请并请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )

A. abc<0 B. -3a+c<0
C. b2-4ac≥0 D. 将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,动点P从点B出发,沿矩形的边由
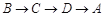 运动,设点P运动的路程为x,
运动,设点P运动的路程为x, 的面积为y,把y看作x的函数,函数的图像如图2所示,则
的面积为y,把y看作x的函数,函数的图像如图2所示,则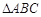 的面积为( )
的面积为( )
A. 10 B. 16 C. 18 D. 20
相关试题

