【题目】如图,平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=![]() cm,OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒
cm,OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒![]() cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
(1)用t的式子表示△OPQ的面积S;
(2)求证:四边形OPBQ的面积是一个定值,并求出这个定值;
(3)当△OPQ与△PAB和△QPB相似时,抛物线y=![]() x 2+bx+c经过B、P两点,过线段BP上一动点M作y轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.
x 2+bx+c经过B、P两点,过线段BP上一动点M作y轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.

参考答案:
【答案】(1)S△OPQ=-![]() t2+
t2+![]() t(0<t<8);(2)四边形OPBQ的面积为一个定值,且等于
t(0<t<8);(2)四边形OPBQ的面积为一个定值,且等于![]() ;(3)3:29 .
;(3)3:29 .
【解析】试题分析:(1)根据![]() 的运动速度,可用
的运动速度,可用![]() 表示出
表示出![]() 的长,进而根据
的长,进而根据![]() 的长求出
的长求出![]() 的表达式,即可由三角形的面积公式得到
的表达式,即可由三角形的面积公式得到![]() 的函数关系式;
的函数关系式;
(2)四边形![]() 的面积,可由矩形
的面积,可由矩形![]() 的面积差求得,进而可得到所求的定值;
的面积差求得,进而可得到所求的定值;
(3)若![]() 与
与![]() 和
和![]() 相似,那么
相似,那么![]() 必为直角三角形,且
必为直角三角形,且![]() 由于
由于![]() 所以这三个相似三角形的对应关系是
所以这三个相似三角形的对应关系是![]() 根据相似三角形得到的比例线段求出
根据相似三角形得到的比例线段求出![]() 的值,进而可确定点P的坐标,求出抛物线和直线
的值,进而可确定点P的坐标,求出抛物线和直线![]() 的解析式;可设
的解析式;可设![]() 点的横坐标为
点的横坐标为![]() ,根据直线
,根据直线![]() 和抛物线的解析式,求出
和抛物线的解析式,求出![]() 的纵坐标,进而可得到关于
的纵坐标,进而可得到关于![]() 的长与
的长与![]() 的函数关系式,根据函数的性质即可求出
的函数关系式,根据函数的性质即可求出![]() 的最大值及对应的
的最大值及对应的![]() 点坐标;设
点坐标;设![]() 与直线
与直线![]() 的交点为
的交点为![]() ,根据
,根据![]() 点的坐标和直线
点的坐标和直线![]() 的解析式即可求出
的解析式即可求出![]() 点的坐标,也就能得到
点的坐标,也就能得到![]() 的长,以
的长,以![]() 为底,
为底, ![]() 横坐标差的绝对值为高,可求出
横坐标差的绝对值为高,可求出![]() 的面积,进而可根据四边形
的面积,进而可根据四边形![]() 的面积求出五边形
的面积求出五边形![]() 的面积,由此可求出它们的比例关系式.
的面积,由此可求出它们的比例关系式.
试题解析:(1)![]()
![]()
∴S△OPQ=![]() (8-t)·
(8-t)·![]() t=-
t=-![]() t2+
t2+![]() t(0<t<8).
t(0<t<8).
(2)∵S四边形OPBQ=S矩形ABCD-S△PAB-S△CBQ.
=8×![]() -
-![]() ×
×![]() t-
t-![]() ×8×(
×8×(![]() -
-![]() t)=
t)=![]() .
.
∴四边形OPBQ的面积为一个定值,且等于![]() .
.
(3)当△OPQ与△PAB和△QPB相似时,△QPB必须是一个直角三角形,依题意只能是∠QPB=90°.
又∵BQ与AO不平行,∴∠QPO不可能等于∠PQB,∠APB不可能等于∠PBQ.
∴根据相似三角形的对应关系只能是△OPQ∽△PBQ∽△ABP.
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得:t=4.
,解得:t=4.
经检验:t=4是方程的解且符合题意(从边长关系和速度考虑)此时P(![]() ,0).
,0).
∵B(![]() ,8)且抛物线y=
,8)且抛物线y=![]() x2+bx+c经过B、P两点,
x2+bx+c经过B、P两点,
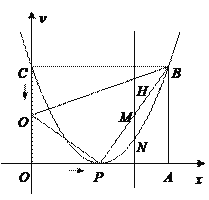
∴抛物线是y=![]() x2-
x2-![]() x+8,直线BP是y=
x+8,直线BP是y=![]() x-8.
x-8.
设M(m, ![]() m-8),则N(m,
m-8),则N(m, ![]() m2-
m2-![]() m+8).
m+8).
∵M是BP上的动点,∴![]() ≤m≤
≤m≤![]() .
.
∵y1=![]() x2-
x2-![]() x+8=
x+8=![]() ( x-
( x-![]() )2.
)2.
∴抛物线的顶点是P(![]() ,0).
,0).
又y1=![]() x2-
x2-![]() x+8与y2=
x+8与y2=![]() x-8交于P、B两点,
x-8交于P、B两点,
∴当![]() ≤m≤
≤m≤![]() 时,y2>y1.
时,y2>y1.
∴|MN |=|y2-y1|=y2-y1=(![]() m-8)-(
m-8)-(![]() m2-
m2-![]() m+8).
m+8).
=-![]() m2+
m2+![]() m-16=-
m-16=-![]() (m-
(m-![]() )2+2.
)2+2.
∴当m=![]() 时,MN有最大值是2,此时M(
时,MN有最大值是2,此时M(![]() ,4).
,4).
设MN与BQ交于H点,则H(![]() ,7).
,7).
∴S△BHM=![]() ×3×
×3×![]() =
=![]() .
.
∴S△BHM:S五边形QOPMH =![]() :(
:(![]() -
-![]() )=3:29.
)=3:29.
∴当线段MN的长取最大值时,直线MN把四边形OPBQ分成两部分的面积之比为3:29 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个全等的直角三角形ABC和DEF重叠在一起,其中∠ACB=∠DFE=90°,∠A=∠FDE=60°,AC=1. 固定△ABC不动,将△DEF进行如下操作:
(1) 如图 (1),△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.
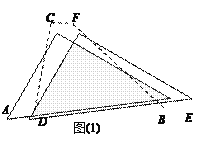
(2)如图(2),当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.

(3)如图(3),△DEF的F点固定在AB的中点,然后绕F点按顺时针方向旋转△DEF,使EF交在AC边上于M,FD交BC于N,若FM=x,FN=y,试求y关于x的函数关系式。

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=40°,则∠ACB的度数为 .
②若∠ACB=128°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长为1个单位长度,建立如图所示的平面直角坐标系,△ABC的顶点均为格点,把△ABC向右平移5个单位长度得到△A1B1C1,再作出△ABC关于x轴对称的△A2B2C2.
(1)在图中画出△A1B1C1和△A2B2C2;
(2)点
 在
在 轴上,且△ABP与△ABC的面积相等,则点P坐标为______;
轴上,且△ABP与△ABC的面积相等,则点P坐标为______;(3)横、纵坐标均为整数的点为整数点,在第二象限中的整数点M满足OM<OC,直接写出整数点
 的所有可能坐标.
的所有可能坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在平面直角坐标系中,作出下列各点,A(-3,4), B(-3,-2),O(0,0),并把各点连起来.
(2)画出△ABO先向下平移2个单位,再向右平移4 个单位得到的图形△A1B1o1,并直接写出A1坐标
(3) 直接写出三角形ABO的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1已知:∠B=25°,∠BED=80°,∠D=55°.探究AB与CD有怎样的位置关系.
(2)如图2已知AB∥EF,试猜想∠B,∠F,∠BCF之间的关系,写出这种关系,并加以证明.
(3)如图3已知AB∥CD,试猜想∠1,∠2,∠3,∠4,∠5之间的关系,请直接写出这种关系,不用证明.



相关试题

