【题目】(1)在平面直角坐标系中,作出下列各点,A(-3,4), B(-3,-2),O(0,0),并把各点连起来.
(2)画出△ABO先向下平移2个单位,再向右平移4 个单位得到的图形△A1B1o1,并直接写出A1坐标
(3) 直接写出三角形ABO的面积.

参考答案:
【答案】A1(1,2) 面积为9
【解析】
(1)根据平面直角坐标系找出点A、B的位置,与点O顺次连接即可;
(2)根据网格结构找出点A、B、O的对应点A1、B1、O1的位置,然后顺次连接即可,根据点A1的位置可直接写出它的坐标;
(3)利用三角形的面积公式列式计算即可得解.
解:(1)如图所示;
(2)△A1B1O1如图所示,A1(1,2);
(3)△ABO的面积=![]() ×(4+2)×3=9.
×(4+2)×3=9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商场采购员要到厂家批发购进篮球和排球共100只,付款总额不得超过11 815元.已知两种球厂家的批发价和商场的零售价如右表,试解答下列问题:
品名
厂家批发价(元/只)
市场零售价(元/只)
篮球
130
160
排球
100
120
(1)该采购员最多可购进篮球多少只?
(2)若该商场把这100只球全部以零售价售出,为使商场获得的利润不低于2580元,则采购员至少要购篮球多少只,该商场最多可盈利多少元? -
科目: 来源: 题型:
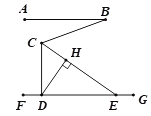
查看答案和解析>>【题目】如图,直线AB∥FG,CE平分∠BCD,交FG于点E,过点D作DH⊥CE,垂足为H,若∠ABC=20°,则∠CEG-∠CDH=________度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.
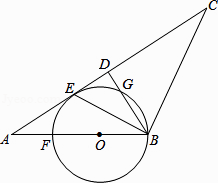
(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)当BD=6,AB=10时,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+6x+c(a≠0)交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,﹣5),点B的坐标为(1,0).
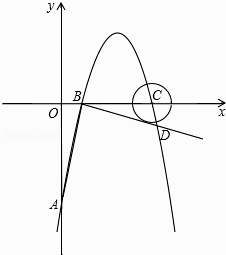
(1)求此抛物线的解析式及定点坐标;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴与⊙C的位置关系,并说明理由;
(3)在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
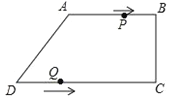
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒2cm的速度沿线段AB向点B方向运动,点Q从点D出发,以每秒3cm的速度沿线段DC向点C运动,已知动点P、Q同时出发,点P到达B点或点Q到达C点时,P、Q运动停止,设运动时间为t (秒).
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求t的值;
(3)在点P、点Q的运动过程中,是否存在某一时刻,使得PQ⊥AB?若存在,请求出t的值并说明理由;若不存在,请说明理

-
科目: 来源: 题型:
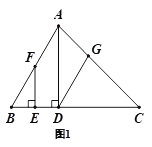
查看答案和解析>>【题目】已知,在三角形ABC中,AD⊥BC于D,F是AB上一点,FE⊥BC于E,∠ADG=∠BFE
(1)如图1,求证:DG∥AB
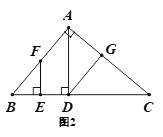
(2)如图2,若∠BAC=90°,请直接写出图中与∠CAD互余的角,不需要证明.
相关试题

