【题目】探究与发现:如图1所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:

(1)观察“规形图”,试探究![]() 与
与![]() 之间的关系,并说明理由;
之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在![]() 上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若
上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若![]() ,则
,则![]() ________;
________;
②如图3,DC平分![]() ,EC平分
,EC平分![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
③如图4,![]() 的10 等分线相交于点
的10 等分线相交于点![]() ,若
,若![]() ,求∠A的度数.
,求∠A的度数.
参考答案:
【答案】(1)∠BDC=∠A+∠B+∠C,理由见解析;(2)①∠ABX+∠ACX=50°;②85°;③63°.
【解析】
(1)首先连接AD并延长至点F,然后根据三角形外角的性质,即可判断出∠BDC=∠A+∠B+∠C;
(2)①由(1)可得∠ABX+∠ACX+∠A=∠BXC,然后根据∠A=40°,∠BXC=90°,求出∠ABX+∠ACX的值是多少即可.
②由(1)可得∠DBE=∠DAE+∠ADB+∠AEB,再根据∠DAE=40°,∠DBE=130°,求出∠ADB+∠AEB的值是多少;然后根据∠DCE=![]() (∠ADB+∠AEB)+∠DAE,求出∠DCE的度数是多少即可.
(∠ADB+∠AEB)+∠DAE,求出∠DCE的度数是多少即可.
③根据∠BG1C=![]() (∠ABD+∠ACD)+∠A,∠BG1C=70°,设∠A为x°,可得∠ABD+∠ACD=133°-x°,解方程,求出x的值,即可判断出∠A的度数是多少.
(∠ABD+∠ACD)+∠A,∠BG1C=70°,设∠A为x°,可得∠ABD+∠ACD=133°-x°,解方程,求出x的值,即可判断出∠A的度数是多少.
解:(1)如图(1),连接AD并延长至点F,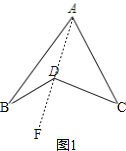 ,
,
根据三角形外角的性质,可得
∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD,
又∵∠BDC=∠BDF+∠CDF,∠BAC=∠BAD+∠CAD,
∴∠BDC=∠A+∠B+∠C.
(2)①由(1),可得
∠ABX+∠ACX+∠A=∠BXC,
∵∠A=40°,∠BXC=90°,
∴∠ABX+∠ACX=90°-40°=50°.
②由(1),可得
∠DBE=∠DAE+∠ADB+∠AEB,
∴∠ADB+∠AEB=∠DBE-∠DAE=130°-40°=90°,
∴![]() (∠ADB+∠AEB)=90°÷2=45°,
(∠ADB+∠AEB)=90°÷2=45°,
∴∠DCE=![]() (∠ADB+∠AEB)+∠DAE
(∠ADB+∠AEB)+∠DAE
=45°+40°
=85°.
③∠BG1 C=![]() (∠ABD+∠ACD)+∠A,
(∠ABD+∠ACD)+∠A,
∵∠BG1 C=70°,
∴设∠A为x°,
∵∠ABD+∠ACD=133°-x°
∴![]() (133-x)+x=70,
(133-x)+x=70,
∴13.3-![]() x+x=70,
x+x=70,
解得x=63,即∠A的度数为63°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不透明的口袋中装有大小、形状完全相同的2个白球 ,a个红球.
(1)若从中任意摸出1个球,“是白球”的概率为
 ,则a=_____.
,则a=_____.(2)在(1)的条件下,从中任意摸出2个球 ,求“两个球的颜色相同”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的方格纸中,小正方形的顶点叫做格点,
 是一个格点三角形(即
是一个格点三角形(即 的三个顶点都在格点上),根据要求回答下列问题:
的三个顶点都在格点上),根据要求回答下列问题: 画出
画出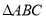 先向左平移6格,再向上平移
先向左平移6格,再向上平移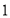 格所得的
格所得的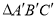 ;
; 利用网格画出
利用网格画出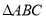 中
中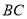 边上的高
边上的高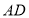 .
.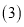 过点
过点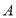 画直线,将
画直线,将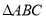 分成面积相等的两个三角形;
分成面积相等的两个三角形;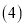 画出与
画出与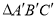 有一条公共边,且与
有一条公共边,且与 全等的格点三角形.
全等的格点三角形.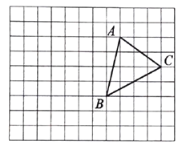
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学计划购进若干个甲种规格的排球和乙种规格的足球. 如果购买20个甲种规格的排球和15个乙种规格的足球,一共需要花费2050元;如果购买10个甲种规格的排球和20个乙种规格的足球,一共需要花费1900元。
(1)求每个甲种规格的排球和每个已汇总规格的足球的价格分别是多少元?
(2)如果学校要购买甲种规格的排球和乙种规格的足球共50个,并且预算总费用不超过3080元,那么该学校至多能购买多少个乙种规格的足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1的小正方形网格中,△AOB的顶点均在格点上.
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,A1的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型, A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2),请回答下列问题:
(1)在这次调查中D类型有多少名学生?
(2)写出被调查学生每人植树量的众数、中位数;
(3)求被调查学生每人植树量的平均数,并估计这260名学生共植树多少棵?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠MON内的一点,过点P作PA⊥OM于点A,PB⊥ON于点B,且OA=OB.
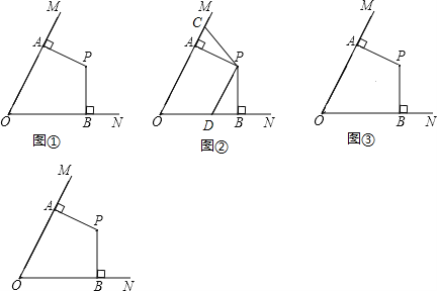
(1)求证:PA=PB;
(2)如图②,点C是射线AM上一点,点D是线段OB上一点,且∠CPD+∠MON=180°,若OC=8,OD=5.求线段OA的长.
(3)如图③,若∠MON=60°,将PB绕点P以每秒2°的速度顺时针旋转,12秒后,PA开始绕点P以每秒10°的速度顺时针旋转,PA旋转270°后停止,此时PB也随之停止旋转.旋转过程中,PA所在直线与OM所在直线的交点记为G,PB所在直线与ON所在直线的交点记为H.问PB旋转几秒时,PG=PH?
相关试题

