【题目】我市某中学计划购进若干个甲种规格的排球和乙种规格的足球. 如果购买20个甲种规格的排球和15个乙种规格的足球,一共需要花费2050元;如果购买10个甲种规格的排球和20个乙种规格的足球,一共需要花费1900元。
(1)求每个甲种规格的排球和每个已汇总规格的足球的价格分别是多少元?
(2)如果学校要购买甲种规格的排球和乙种规格的足球共50个,并且预算总费用不超过3080元,那么该学校至多能购买多少个乙种规格的足球?
参考答案:
【答案】(1)每个排球50元,每个足球70元;(2)至多购买足球29个
【解析】
(1)设每个甲种规格的排球的价格是x元,每个乙种规格的足球的价格是y元,根据“购买20个甲种规格的排球和15个乙种规格的足球,一共需要花费2050元;购买10个甲种规格的排球和20个乙种规格的足球,一共需要花费1900元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买乙种规格的足球m个,则购买甲种规格的排球(50m)个,根据预算总费用不超过3080元,即可得出关于m的一元一次不等式,解之即可得出结论.
解:(1)设每个甲种规格的排球的价格是x元,每个乙种规格的足球的价格是y元,
根据题意得:![]() ,
,
解这个方程组得:![]() ,
,
答:每个甲种规格的排球的价格是50元,每个乙种规格的足球的价格是70元;
(2)设该学校购买m个乙种规格的足球,则购买甲种规格的排球(50m)个,
根据题意得:50(50m)+70m≤3080,
解得:m≤29,
答:该学校至多能购买29个乙种规格的足球.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=﹣3是关于x的方程(k+3)x+2=3x﹣2k的解.
(1)求k的值;
(2)在(1)的条件下,已知线段AB=6cm,点C是直线AB上一点,且BC=kAC,若点D是AC的中点,求线段CD的长.
-
科目: 来源: 题型:
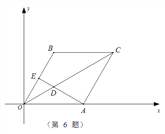
查看答案和解析>>【题目】在如图直角坐标系内,四边形AOBC是边长为2的菱形,E为边OB的中点,连结AE与对角线OC交于点D,且∠BCO=∠EAO,则点D坐标为( )
A. (
 ,
, ) B. (1,
) B. (1, ) C. (
) C. ( ,
, ) D. (1,
) D. (1, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠AFC,以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°—∠ABD;④∠BDC=
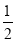 ∠BAC,其中正确的结论有_____________。
∠BAC,其中正确的结论有_____________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
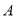 ,点
,点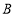 是直线上的两点,
是直线上的两点,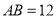 厘米,点
厘米,点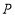 ,点
,点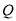 是直线上的两个动点,点
是直线上的两个动点,点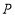 的速度为1厘米/秒,点
的速度为1厘米/秒,点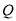 的速度为2厘米/秒.点
的速度为2厘米/秒.点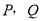 分别从点
分别从点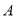 ,点
,点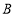 同时相向出发沿直线运动
同时相向出发沿直线运动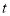 秒:
秒:(1)求
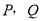 两点刚好重合时的
两点刚好重合时的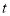 值;
值;(2)当
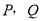 两点重合后继续沿原来方向前进,求相距6厘米时的
两点重合后继续沿原来方向前进,求相距6厘米时的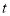 值;
值;(3)当点
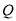 离
离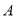 点的距离为2厘米时,求点
点的距离为2厘米时,求点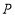 离
离 点的距离.
点的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了传承优秀传统文化,市里组织了一次“汉字听写”大赛,我区有1200名初三学生参加区级初赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:

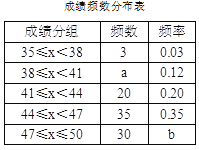
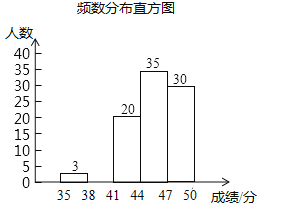
请根据所提供的信息解答下列问题:
(1)样本的中位数是________分;
(2)若按成绩分组情况绘制成扇形统计图,则表示47≤x≤50这组的扇形圆心角为_______°;
(3)请补全频数分布直方图;
(4)请根据抽样统计结果,估计我区初赛中成绩不低于41分的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,点E是边CD的中点,连接BE并延长,交AD延长线于点F,连接BD、CF.
(1)求证:△CEB≌△DEF;
(2)若AB=BF,试判断四边形BCFD的形状,并证明.

相关试题

