【题目】如图,点P是∠MON内的一点,过点P作PA⊥OM于点A,PB⊥ON于点B,且OA=OB.
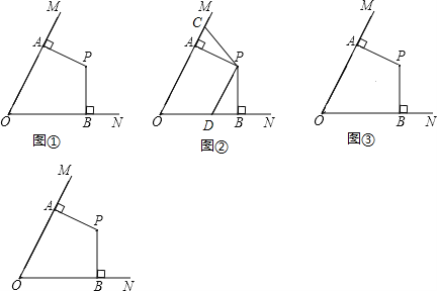
(1)求证:PA=PB;
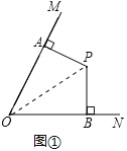
(2)如图②,点C是射线AM上一点,点D是线段OB上一点,且∠CPD+∠MON=180°,若OC=8,OD=5.求线段OA的长.
(3)如图③,若∠MON=60°,将PB绕点P以每秒2°的速度顺时针旋转,12秒后,PA开始绕点P以每秒10°的速度顺时针旋转,PA旋转270°后停止,此时PB也随之停止旋转.旋转过程中,PA所在直线与OM所在直线的交点记为G,PB所在直线与ON所在直线的交点记为H.问PB旋转几秒时,PG=PH?
参考答案:
【答案】(1)见解析;(2)OA=6.5;(3)满足条件的t的值为15s或25s或37.5s.
【解析】
(1)如图1中,连接OP,证明Rt△OPA≌Rt△OPB(HL)即可解决问题.
(2)如图②中,想办法证明OC+OD=2OA即可解决问题.
(3)设点P的旋转时间为t秒.分四种情形①当0<t<12时,不存在.②当12≤t<21时,如图3-1中.③当21≤t<30时,如图3-2中.④当30≤t<39时,如图3-3中,分别求解即可解决问题.
(1)证明:如图①中,连接OP.
∵PA⊥OM,PB⊥ON,
∴∠OAP=∠OBP=90°,
∵OA=OB,OP=OP,
∴Rt△OPA≌Rt△OPB(HL),
∴PA=PB.
(2)如图②中,
∵∠PAO=∠PBO=90°,
∴∠AOB+∠APB=180°,
∵∠CPD+∠AOB=180°,
∴∠CPD=∠APB,
∴∠APC=∠BPD,
∵PA=PB,∠PAC=∠PBD=90°,
∴△PAC≌△PBD(ASA),
∴AC=BD,
∴OC+OD=OA+AC+OB-BD=2OA=13,
∴OA=6.5.
(3)设点P的旋转时间为t秒.
①当0<t<12时,此时只有PB旋转,PA没有旋转,故不存在PG=PH.
②当PA旋转的度数为0°—90°时,时间t的取值为:12≤t<21;
∴当12≤t<21时,如图3-1中,∠APG=(10t-120)°,∠BPH=2t°,
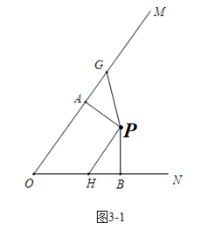
当∠APG=∠BPH时,△PAG≌△PBH,可得PG=PH,
此时10t-120=2t,
∴t=15.
③当PA旋转的度数为90°—180°时,时间t的取值为:21≤t<30,
∴当21≤t<30时,如图3-2中,∠APG=180°-∠APA′=180°-(10t-120)°=(300-10t)°,∠BPH=2t,
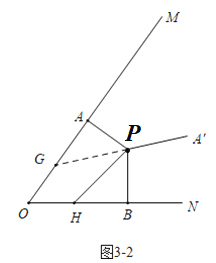
当∠APG=∠BPH时,△PAG≌△PBH,可得PG=PH,
此时300-10t=2t,
∴t=25.
④当PA旋转的度数为180°—270°时,时间t的取值为:30≤t<39;
当30≤t<39时,如图3-3中,∠APG=(10t-300)°,∠BPH=2t,
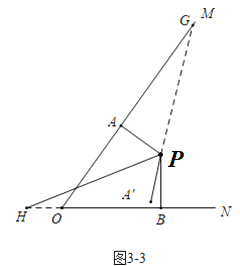
当∠APG=∠BPH时,△PAG≌△PBH,可得PG=PH,
此时10t-300=2t,
∴t=37.5;
综上所述,满足条件的t的值为15s或25s或37.5s.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究与发现:如图1所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:

(1)观察“规形图”,试探究
 与
与 之间的关系,并说明理由;
之间的关系,并说明理由;(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在
 上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若
上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若 ,则
,则 ________;
________;②如图3,DC平分
 ,EC平分
,EC平分 ,若
,若 ,求
,求 的度数;
的度数;③如图4,
 的10 等分线相交于点
的10 等分线相交于点 ,若
,若 ,求∠A的度数.
,求∠A的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1的小正方形网格中,△AOB的顶点均在格点上.
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,A1的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型, A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2),请回答下列问题:
(1)在这次调查中D类型有多少名学生?
(2)写出被调查学生每人植树量的众数、中位数;
(3)求被调查学生每人植树量的平均数,并估计这260名学生共植树多少棵?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某农场去年计划生产玉米和小麦共200吨.采用新技术后,实际产量为225吨,其中玉米超产5%,小麦超产15%.该农场去年实际生产玉米、小麦各多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E为AB边上一点,DE=DC,点F为线段DE上一点,满足∠DFC=∠A,连结CE.
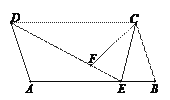
(1)求证:AD=FC;
(2)求证:CE是∠BCF的角平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN为一电视塔,AB是坡角为30°的小山坡(电视塔的底部N与山坡的坡脚A在同一水平线上,被一个人工湖隔开),某数学兴趣小组准备测量这座电视塔的高度.在坡脚A处测得塔顶M的仰角为45°;沿着山坡向上行走40m到达C处,此时测得塔顶M的仰角为30°,请求出电视塔MN的高度.(参考数据:
 ≈1.41,
≈1.41,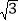 ≈1.73,结果保留整数)
≈1.73,结果保留整数)
相关试题

