【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( ) 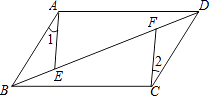
A.BE=DF
B.BF=DE
C.AE=CF
D.∠1=∠2
参考答案:
【答案】C
【解析】解:A、当BE=FD,
∵平行四边形ABCD中,
∴AB=CD,∠ABE=∠CDF,
在△ABE和△CDF中 ,
,
∴△ABE≌△CDF(SAS),故此选项错误;
C、当AE=CF无法得出△ABE≌△CDF,故此选项符合题意;
B、当BF=ED,
∴BE=DF,
∵平行四边形ABCD中,
∴AB=CD,∠ABE=∠CDF,
在△ABE和△CDF中 ,
,
∴△ABE≌△CDF(SAS),故此选项错误;
D、当∠1=∠2,
∵平行四边形ABCD中,
∴AB=CD,∠ABE=∠CDF,
在△ABE和△CDF中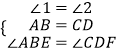 ,
,
∴△ABE≌△CDF(ASA),故此选项错误;
故选C.
【考点精析】掌握平行四边形的性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人共同解方程组
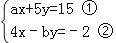 , 由于甲错了方程①中的a,得到方程组的解为
, 由于甲错了方程①中的a,得到方程组的解为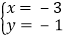 ;乙看错了方程②中的b,得到方程组的解为
;乙看错了方程②中的b,得到方程组的解为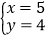 ,
,
(1)求出a,b的值;
(2)求2a﹣3b+5的立方根;
(3)此方程组正确的解应该是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形
 ,点
,点 在边
在边 上,点
上,点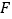 在线段
在线段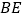 的延长线上,且
的延长线上,且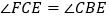 .
.(1)如图1,当点
 为
为 边的中点时,求证:
边的中点时,求证: ;
;(2)如图2,当点
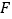 位于线段
位于线段 的延长线上,求证:
的延长线上,求证: .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx﹣3交x轴于B、C两点,且B的坐标为(﹣2,0)直线y=mx+n过点B和抛物线上另一点A(4,3)
(1)求抛物线和直线的解析式;
(2)若点P为抛物线上的一个动点,且在直线AB下方,过P作PQ∥x轴,且PQ=4(点Q在P点右侧).以PQ为一边作矩形PQEF,且点E在直线AB上.求矩形PQEF的最大值.并求出此时点P的坐标;
(3)如图2,在(2)的结论下,连接AP、BP,设QE交于x轴于点D,现即将矩形PQEF沿射线DB以每秒1个单位长度的速度平移,当点D到达点B时停止,记平移时间为t,平移后的矩形PQEF为P′Q′E′F′,且Q′E′分别交直线AB、x轴于N、D′,设矩形P′Q′E′F′与△ABP的重叠部分面积为s,当NA=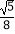 ND′时,求s的值.
ND′时,求s的值.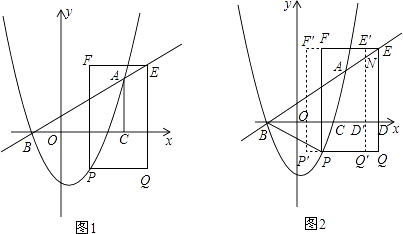
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
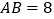 ,⊙
,⊙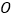 经过点
经过点 、
、 .以
.以 为一边画平行四边形
为一边画平行四边形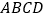 ,另一边
,另一边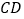 经过点
经过点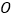 (如图1).以点
(如图1).以点 为圆心,
为圆心,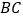 为半径画弧,交线段
为半径画弧,交线段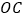 于点
于点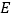 (点
(点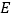 不与点
不与点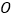 、点
、点 重合).
重合).(1)求证:
 ;
;(2)如果⊙
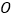 的半径长为
的半径长为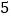 (如图2),设
(如图2),设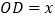 ,
, ,求
,求 关于
关于 的函数解析式,并写出它的定义域;
的函数解析式,并写出它的定义域;(3)如果⊙
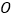 的半径长为
的半径长为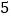 ,联结
,联结 ,当
,当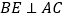 时,求
时,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,M为边AB上的点,且AM=
 BM,延长MB至点E,使ME=MC,连接EC,则点M到直线CE的距离是( )
BM,延长MB至点E,使ME=MC,连接EC,则点M到直线CE的距离是( ) 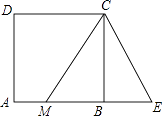
A.2
B.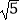
C.5
D.2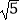
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,EF=2
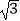 ,则AB的长为 .
,则AB的长为 . 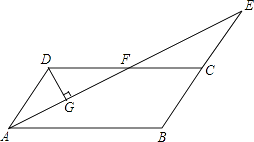
相关试题

