【题目】如图,在ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,EF=2 ![]() ,则AB的长为 .
,则AB的长为 . 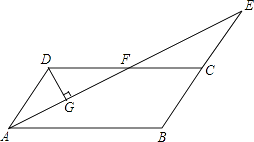
参考答案:
【答案】4
【解析】解:∵AE为∠DAB的平分线,
∴∠DAE=∠BAE,
∵DC∥AB
∴∠BAE=∠DFA,
∴∠DAE=∠DFA,
∴AD=FD,
又∵F为DC的中点,
∴DF=CF,
∴AD=DF= ![]() DC=
DC= ![]() AB,
AB,
∵DG⊥AE,
∴AG=FG,
∵平行四边形ABCD中,
∴AD∥BC,
∴∠DAF=∠E,∠ADF=∠ECF,
在△ADF和△ECF中, 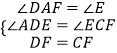 ,
,
∴△ADF≌△ECF(AAS),
∴AF=EF=2 ![]() ,
,
∴AG= ![]() ,
,
∴AD= ![]() =2,
=2,
∴AB=2AD=4;
所以答案是:4.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
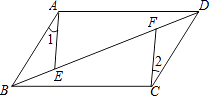
A.BE=DF
B.BF=DE
C.AE=CF
D.∠1=∠2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
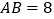 ,⊙
,⊙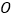 经过点
经过点 、
、 .以
.以 为一边画平行四边形
为一边画平行四边形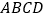 ,另一边
,另一边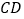 经过点
经过点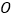 (如图1).以点
(如图1).以点 为圆心,
为圆心,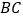 为半径画弧,交线段
为半径画弧,交线段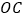 于点
于点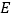 (点
(点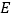 不与点
不与点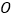 、点
、点 重合).
重合).(1)求证:
 ;
;(2)如果⊙
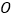 的半径长为
的半径长为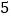 (如图2),设
(如图2),设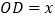 ,
, ,求
,求 关于
关于 的函数解析式,并写出它的定义域;
的函数解析式,并写出它的定义域;(3)如果⊙
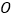 的半径长为
的半径长为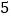 ,联结
,联结 ,当
,当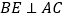 时,求
时,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,M为边AB上的点,且AM=
 BM,延长MB至点E,使ME=MC,连接EC,则点M到直线CE的距离是( )
BM,延长MB至点E,使ME=MC,连接EC,则点M到直线CE的距离是( ) 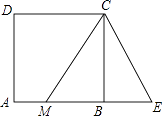
A.2
B.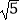
C.5
D.2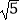
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(k﹣1)x2﹣2kx﹣1=0是关于x的一元二次方程,则k的取值范围是( )
A.k≠﹣1
B.k≠1
C.k≠0
D.k≥1 -
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解一元二次方程 x2+8x+7=0,则方程可变形为( )
A. (x-4)2=9B. (x+4)2=9C. (x-8)2=9D. (x+8)2=9
-
科目: 来源: 题型:
查看答案和解析>>【题目】点(2,6)关于x轴对称点坐标为( )
A.(2,﹣6) B.(﹣2,﹣6) C.(﹣2,6) D.(6,2)
相关试题

