【题目】如图,在边长为4的正方形ABCD中,M为边AB上的点,且AM= ![]() BM,延长MB至点E,使ME=MC,连接EC,则点M到直线CE的距离是( )
BM,延长MB至点E,使ME=MC,连接EC,则点M到直线CE的距离是( ) 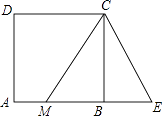
A.2
B.![]()
C.5
D.2 ![]()
参考答案:
【答案】D
【解析】解:如图,作MN⊥EC于N. 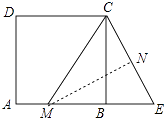
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,∠ABC=90°,
∴AM= ![]() BM,
BM,
∴AM=1,BM=3,
在Rt△BCM中,CM=ME= ![]() =
= ![]() =5,
=5,
∴BE=5﹣3=2,
∴CE= ![]() =
= ![]() =2
=2 ![]()
∵ ![]() MECB=
MECB= ![]() CEMN,
CEMN,
∴MN= ![]() =
= ![]() =2
=2 ![]() ,
,
故选D.
【考点精析】本题主要考查了点到直线的距离和正方形的性质的相关知识点,需要掌握从直线外一点到这条直线的垂线段的长度叫做点到直线的距离;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx﹣3交x轴于B、C两点,且B的坐标为(﹣2,0)直线y=mx+n过点B和抛物线上另一点A(4,3)
(1)求抛物线和直线的解析式;
(2)若点P为抛物线上的一个动点,且在直线AB下方,过P作PQ∥x轴,且PQ=4(点Q在P点右侧).以PQ为一边作矩形PQEF,且点E在直线AB上.求矩形PQEF的最大值.并求出此时点P的坐标;
(3)如图2,在(2)的结论下,连接AP、BP,设QE交于x轴于点D,现即将矩形PQEF沿射线DB以每秒1个单位长度的速度平移,当点D到达点B时停止,记平移时间为t,平移后的矩形PQEF为P′Q′E′F′,且Q′E′分别交直线AB、x轴于N、D′,设矩形P′Q′E′F′与△ABP的重叠部分面积为s,当NA=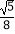 ND′时,求s的值.
ND′时,求s的值.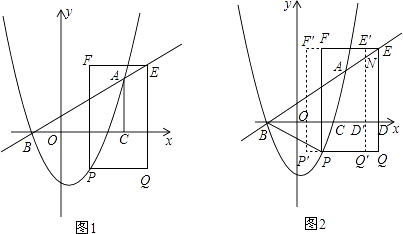
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
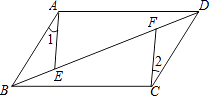
A.BE=DF
B.BF=DE
C.AE=CF
D.∠1=∠2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
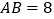 ,⊙
,⊙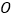 经过点
经过点 、
、 .以
.以 为一边画平行四边形
为一边画平行四边形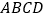 ,另一边
,另一边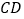 经过点
经过点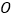 (如图1).以点
(如图1).以点 为圆心,
为圆心,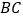 为半径画弧,交线段
为半径画弧,交线段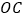 于点
于点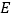 (点
(点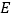 不与点
不与点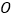 、点
、点 重合).
重合).(1)求证:
 ;
;(2)如果⊙
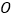 的半径长为
的半径长为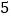 (如图2),设
(如图2),设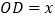 ,
, ,求
,求 关于
关于 的函数解析式,并写出它的定义域;
的函数解析式,并写出它的定义域;(3)如果⊙
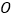 的半径长为
的半径长为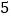 ,联结
,联结 ,当
,当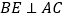 时,求
时,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,EF=2
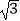 ,则AB的长为 .
,则AB的长为 . 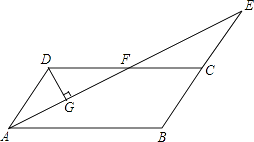
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(k﹣1)x2﹣2kx﹣1=0是关于x的一元二次方程,则k的取值范围是( )
A.k≠﹣1
B.k≠1
C.k≠0
D.k≥1 -
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解一元二次方程 x2+8x+7=0,则方程可变形为( )
A. (x-4)2=9B. (x+4)2=9C. (x-8)2=9D. (x+8)2=9
相关试题

