Question

【题目】如图，已知直角三角形的三边长分别为a、b、c，以直角三角形的三边为边（或直径），分别向外作等边三角形、半圆、等腰直角三角形和正方形。那么，这四个图形中，其面积满足的个数是(　 )

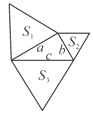
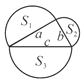
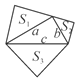
A. 1 B. 2 C. 3 D. 4

Answer 1

【答案】D

【解析】利用直角△ABC的边长就可以表示出等边三角形S1、S2、S3的大小，满足勾股定理；利用圆的面积公式表示出S1、S2、S3，然后根据勾股定理即可解答；在勾股定理的基础上结合等腰直角三角形的面积公式，运用等式的性质即可得出结论；分别用AB、BC和AC表示出 S1、S2、S3，然后根据AB2=AC2+BC2即可得出S1、S2、S3的关系．

设直角三角形ABC的三边AB、CA、BC的长分别为a、b、c，则c2=a2+b2.

第一幅图：∵S3=c2，S1=a2，S2=b2

∴S1+S2= (a2+b2)＝c2=S3；

第二幅图：由圆的面积计算公式知：S3=，S2=，S1=，

则S1+S2=+== S3;

第三幅图：由等腰直角三角形的性质可得：S3=c2，S2=b2，S1=a2，

则S3+S2=(a2+b2)=c2=S1．

第四幅图：因为三个四边形都是正方形则：

∴S3=BC2=c2，S2= AC2=b2，，S1=AB2=a2，

∴S3+S2=a2+b2=c2=S1．

故选：D.