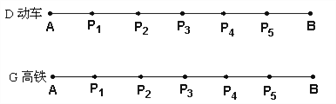
【题目】以下是两张不同类型火车的车票(“![]() 次”表示动车,“
次”表示动车,“![]() 次”表示高铁):
次”表示高铁):

(1)根据车票中的信息填空:该列动车和高铁是__________向而行(填“相”或“同”).
(2)已知该列动车和高铁的平均速度分别为![]() 、
、![]() ,两列火车的长度不计.
,两列火车的长度不计.
①经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到![]() ,求
,求![]() 、
、![]() 两地之间的距离.
两地之间的距离.
②在①中测算的数据基础上,已知![]() 、
、![]() 两地途中依次设有
两地途中依次设有![]() 个站点
个站点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,且
,且![]() ,动车每个站点都停靠,高铁只停靠
,动车每个站点都停靠,高铁只停靠![]() 、
、![]() 两个站点,两列火车在每个停靠站点都停留
两个站点,两列火车在每个停靠站点都停留![]() .求该列高铁追上动车的时刻.
.求该列高铁追上动车的时刻.
参考答案:
【答案】(1)同;(2)①1200km,②8点55分.
【解析】试题分析:(1)由车票可以得出动车和高铁都是由A地开往B地,所以动车和高铁是同向而行;(2)高铁比动车晚出发1个小时,所以动车比高铁全程多花了2个小时,设A、B两地距离为xkm,则可列方程![]() -
-![]() =2,解出x即可;(3)每个相邻站点距离为:1200÷6=200km,
=2,解出x即可;(3)每个相邻站点距离为:1200÷6=200km,
高铁到每站所花时间为:200÷300=![]() h=40min,动车到每站所花时间为:200÷200=1h=60min,
h=40min,动车到每站所花时间为:200÷200=1h=60min,
画出动车和高铁到每一站的时间图,由此可以得出高铁在P2、P3之间追上并超过动车,设高铁经过y小时后追上动车,则(y-![]() )×300=(y+1-
)×300=(y+1-![]() ×2)×200,解得y=
×2)×200,解得y=![]() .
.
所以高铁在经过![]() h后可以追上动车,追上的时刻为8点55分.
h后可以追上动车,追上的时刻为8点55分.
试题解析:
(1)同;
(2)①设A、B两地距离为xkm,则
![]() -
-![]() =2,解得x=1200,
=2,解得x=1200,
所以A、B两地之间的距离为1200km;
②每个相邻站点距离为:1200÷6=200km,
高铁到每站所花时间为:200÷300=![]() h=40min,动车到每站所花时间为:200÷200=1h=60min,
h=40min,动车到每站所花时间为:200÷200=1h=60min,
所以动车和高铁到每一站的时间如图所示:

由此可以得出高铁在P2、P3之间追上并超过动车,
设高铁经过y小时后追上动车,
则(y-![]() )×300=(y+1-
)×300=(y+1-![]() ×2)×200,解得y=
×2)×200,解得y=![]() .
.
所以高铁在经过![]() h后可以追上动车,追上的时刻为8点55分.
h后可以追上动车,追上的时刻为8点55分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】铁路货运调度站有A、B两个信号灯,在灯这旁停靠着甲、乙、丙三列火车.它们中最长的车长与居中车长之差等于居中车长与最短车长之差,其中乙车的车长居中,最开始的时候,甲、丙两车车尾对齐,且车尾正好位于A信号灯处,而车头则冲着B信号灯的方向,乙车的车尾则位于B信号灯处,车头则冲着A的方向,现在,三列火车同时出发向前行驶,3秒之后三列火车的车头恰好相遇,再过9秒,甲车恰好超过丙车,而丙车也正好完全和乙车错开,请问:甲乙两车从车头相遇直到完全错开一共用了_____秒钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】盛盛同学到某高校游玩时,看到运动场的宣传栏中的部分信息(如下表):
院系篮球赛成绩公告
比赛场次
胜场
负场
积分
22
12
10
34
22
14
8
36
22
0
22
22
盛盛同学结合学习的知识设计了如下问题,请你帮忙完成下列问题:
(1)从表中可以看出,负一场积______分,胜一场积_______分;
(2)某队在比完22场的前提下,胜场总积分能等于其负场总积分的2倍吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.
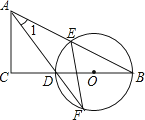
(1)求证:∠1=∠F.
(2)若sinB=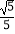 ,EF=2
,EF=2 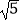 ,求CD的长.
,求CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=60°,BC=2,CD是△ABC的一条高线.若E,F分别是CD和BC上的动点,则BE+EF的最小值是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠,点A的对应点为点G.
(1)填空:如图1,当点G恰好在BC边上时,四边形ABGE的形状是___________形;
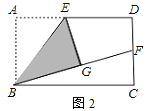
(2)如图2,当点G在矩形ABCD内部时,延长BG交DC边于点F.
 求证:BF=AB+DF;
求证:BF=AB+DF; 若AD=
若AD=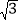 AB,试探索线段DF与FC的数量关系.
AB,试探索线段DF与FC的数量关系.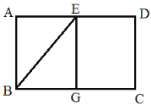
-
科目: 来源: 题型:
查看答案和解析>>【题目】高铁的开通,给泰安市民出行带来了极大的方便,五一期间,乐乐和颖颖相约到青岛市某游乐场游玩,乐乐乘私家车从泰安出发1小时后,颖颖乘坐高铁从泰安出发,先到青岛火车站,然后转乘出租车到游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开泰安的距离y(千米)与时间t(小时)的关系如图所示,请结合图象解决下面问题.
(1)高铁的平均速度是每小时多少千米;
(2)当颖颖到达青岛火车站时,乐乐距离游乐园还有多少千米?

相关试题

