搜索
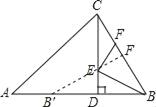
【题目】如图，在△ABC中，∠ABC=60°，BC=2，CD是△ABC的一条高线．若E，F分别是CD和BC上的动点，则BE+EF的最小值是_____．
参考答案：
【答案】
．
【解析】
作B关于CD的对称点B′，过B′作B′F⊥BC于F交CD于E，则B′F的长度即为BE+EF的最小值，根据直角三角形的性质得到BD=
CD，根据已知条件得到BB′=BC，推出△CDB≌△BB′F，于是得到B′F=CD．
作B关于CD的对称点B′，过B′作B′F⊥BC于F交CD于E，
则B′F的长度即为BE+EF的最小值，
∵∠ABC=60°，CD⊥AB，
∴∠BCD=30°，
∴BD=CD，
∵BD=BB′，
∴BB′=BC，
在△CDB与△B′FB中，
，
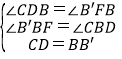∴△CDB≌△BB′F，（AAS）
∴B′F=CD=
BC=．
故答案是：．
-
科目： 来源： 题型：
查看答案和解析>>【题目】盛盛同学到某高校游玩时，看到运动场的宣传栏中的部分信息（如下表）：
院系篮球赛成绩公告
比赛场次
胜场
负场
积分
22
12
10
34
22
14
8
36
22
0
22
22
盛盛同学结合学习的知识设计了如下问题，请你帮忙完成下列问题：
（1）从表中可以看出，负一场积______分,胜一场积_______分；
（2）某队在比完22场的前提下，胜场总积分能等于其负场总积分的2倍吗？请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°，D是BC边上一点，以DB为直径的⊙O经过AB的中点E，交AD的延长线于点F，连结EF．
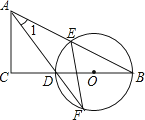
（1）求证：∠1=∠F．
（2）若sinB=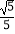
，EF=2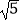 
，求CD的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】以下是两张不同类型火车的车票（“
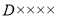次”表示动车，“
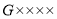次”表示高铁）：
（1）根据车票中的信息填空：该列动车和高铁是__________向而行（填“相”或“同”）．
（2）已知该列动车和高铁的平均速度分别为
、
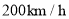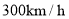，两列火车的长度不计．①经过测算，如果两列火车直达终点（即中途都不停靠任何站点），高铁比动车将早到
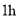，求
、
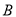两地之间的距离．②在①中测算的数据基础上，已知
、
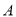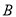两地途中依次设有
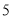个站点
、
、
、
、
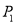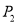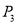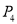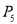，且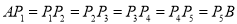
，动车每个站点都停靠，高铁只停靠
、
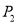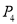两个站点，两列火车在每个停靠站点都停留
．求该列高铁追上动车的时刻．
-
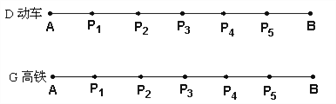
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，E是AD的中点，将△ABE沿BE折叠，点A的对应点为点G.
（1）填空：如图1，当点G恰好在BC边上时，四边形ABGE的形状是___________形；
（2）如图2，当点G在矩形ABCD内部时，延长BG交DC边于点F.
求证：BF=AB+DF；
若AD=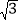
AB，试探索线段DF与FC的数量关系.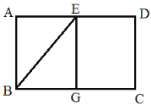
-
科目： 来源： 题型：
查看答案和解析>>【题目】高铁的开通，给泰安市民出行带来了极大的方便，五一期间，乐乐和颖颖相约到青岛市某游乐场游玩，乐乐乘私家车从泰安出发1小时后，颖颖乘坐高铁从泰安出发，先到青岛火车站，然后转乘出租车到游乐园（换车时间忽略不计），两人恰好同时到达游乐园，他们离开泰安的距离y（千米）与时间t（小时）的关系如图所示，请结合图象解决下面问题．
（1）高铁的平均速度是每小时多少千米；
（2）当颖颖到达青岛火车站时，乐乐距离游乐园还有多少千米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用
，
表示直角三角形的两直角边（
），下列四个说法：
①
，②
，③
，④
.其中说法正确的是 …………………………………………………………（ ）
A. ①② B. ①②③ C. ①②④ D. ①②③④
相关试题
