【题目】如图所示,画一个长和宽分别为![]() 、
、![]() 的长方形,并将其按一定的方式进行旋转.
的长方形,并将其按一定的方式进行旋转.

![]() 你能得到几种不同的圆柱体?
你能得到几种不同的圆柱体?
![]() 把一个平面图形旋转成几何体,必须明确哪两个条件?
把一个平面图形旋转成几何体,必须明确哪两个条件?
参考答案:
【答案】(1)四种不同的圆柱体;(2)旋转轴和旋转角这两个条件.
【解析】
(1)分别以长方形的长和宽所在直线为旋转轴,旋转360°;以对边的中点连线所在直线为旋转轴,旋转180°;
(2)需要说明旋转轴和旋转角这两个条件.
解:![]() 由于长和宽分别为
由于长和宽分别为![]() 、
、![]() 的长方形,旋转可得到四种不同的圆柱体;
的长方形,旋转可得到四种不同的圆柱体;
①一长方形的一条长![]() (或
(或![]() )所在直线为旋转轴,旋转
)所在直线为旋转轴,旋转![]() ,可得到底面半径为
,可得到底面半径为![]() ,高为
,高为![]() 的圆柱体;
的圆柱体;
②一长方形的一条宽![]() (或
(或![]() )所在直线为旋转轴,旋转一周,可得到底面半径为
)所在直线为旋转轴,旋转一周,可得到底面半径为![]() ,高为
,高为![]() 的圆柱体;
的圆柱体;
③以长方形的长![]() 、
、![]() 的中点
的中点![]() 、
、![]() 所在直线为旋转轴,旋转
所在直线为旋转轴,旋转![]() ,可得到底面半径为
,可得到底面半径为![]() ,高为
,高为![]() 的圆柱体;
的圆柱体;
④以长方形的长![]() 、
、![]() 的中点
的中点![]() 、
、![]() 所在直线为旋转轴,旋转
所在直线为旋转轴,旋转![]() ,可得到底面半径为
,可得到底面半径为![]() ,高为
,高为![]() 的圆柱体;
的圆柱体;

![]() 把一个平面图形旋转成几何体,需要说明旋转轴和旋转角这两个条件.
把一个平面图形旋转成几何体,需要说明旋转轴和旋转角这两个条件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从A点出发向北偏东60°方向走了80m米到达B地,从B地他又向西走了160m到达C地.
(1)用1:4000的比例尺(即图上1cm等于实际距离40m)画出示意图,并标上字母;
(2)用刻度尺出AC的距离(精确到0.01cm),并求出C但距A点的实际距离(精确到1m);
(3)用量角器测出C点相对于点A的方位角.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是由些棱长
 的正方体小木块搭建成的几何体的主视图、俯视图和左视图,①请你观察它是由多少块小木块组成的;②在俯视图中标出相应位置立方体的个数;③求出该几何体的表面积(包含底面).
的正方体小木块搭建成的几何体的主视图、俯视图和左视图,①请你观察它是由多少块小木块组成的;②在俯视图中标出相应位置立方体的个数;③求出该几何体的表面积(包含底面).
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣
 x2+bx+c与x轴分别交于点A(﹣2,0)、B(4,0),与y轴交于点C.
x2+bx+c与x轴分别交于点A(﹣2,0)、B(4,0),与y轴交于点C.
(1)求抛物线解析式;
(2)求△CAB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC与BD相交于O,∠1=∠4,∠2=∠3,△ABC的周长为25cm,△AOD的周长为17cm,则AB=( )
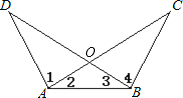
A. 4cm ; B. 8cm; C. 12cm; D. 无法确定;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,CE∥BF,
A. E、F、D在一直线上,BC与AD交于点O,且OE=OF,则图中有全等三角形的对数为( )
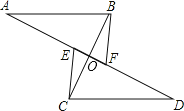
A. 2
B. 3
C. 4
D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.

(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
相关试题

