【题目】抛物线y=﹣ ![]() x2+bx+c与x轴分别交于点A(﹣2,0)、B(4,0),与y轴交于点C.
x2+bx+c与x轴分别交于点A(﹣2,0)、B(4,0),与y轴交于点C.
(1)求抛物线解析式;
(2)求△CAB的面积.
参考答案:
【答案】
(1)解:将(﹣2,0),(4,0)代入函数解析式中得 ![]() ,
,
解得:b=1,c=4.所以y=﹣ ![]() x2+x+4
x2+x+4
(2)解:当x=0时,y=4.所以C(0,4),AB=6.
S△ABC= ![]() ABOC=
ABOC= ![]() ×6×4=12
×6×4=12
【解析】(1)将(﹣2,0),(4,0)代入函数解析式,列出b和c的二元一次方程组,求出b和c的值;(2)首先求出点C的坐标,再求出AB的长,利用三角形面积公式求出答案即可.
【考点精析】掌握抛物线与坐标轴的交点是解答本题的根本,需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=90°,AB=BC=2,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,那么BM的长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从A点出发向北偏东60°方向走了80m米到达B地,从B地他又向西走了160m到达C地.
(1)用1:4000的比例尺(即图上1cm等于实际距离40m)画出示意图,并标上字母;
(2)用刻度尺出AC的距离(精确到0.01cm),并求出C但距A点的实际距离(精确到1m);
(3)用量角器测出C点相对于点A的方位角.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是由些棱长
 的正方体小木块搭建成的几何体的主视图、俯视图和左视图,①请你观察它是由多少块小木块组成的;②在俯视图中标出相应位置立方体的个数;③求出该几何体的表面积(包含底面).
的正方体小木块搭建成的几何体的主视图、俯视图和左视图,①请你观察它是由多少块小木块组成的;②在俯视图中标出相应位置立方体的个数;③求出该几何体的表面积(包含底面).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,画一个长和宽分别为
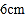 、
、 的长方形,并将其按一定的方式进行旋转.
的长方形,并将其按一定的方式进行旋转.
 你能得到几种不同的圆柱体?
你能得到几种不同的圆柱体? 把一个平面图形旋转成几何体,必须明确哪两个条件?
把一个平面图形旋转成几何体,必须明确哪两个条件? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC与BD相交于O,∠1=∠4,∠2=∠3,△ABC的周长为25cm,△AOD的周长为17cm,则AB=( )
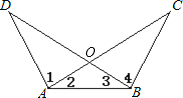
A. 4cm ; B. 8cm; C. 12cm; D. 无法确定;
-
科目: 来源: 题型:
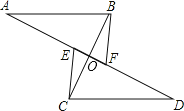
查看答案和解析>>【题目】如图,AB∥CD,CE∥BF,
A. E、F、D在一直线上,BC与AD交于点O,且OE=OF,则图中有全等三角形的对数为( )
A. 2
B. 3
C. 4
D. 5
相关试题

