【题目】如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC. 
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
参考答案:
【答案】
(1)解:∵BC=DC,
∴∠CBD=∠CDB=39°,
∵∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,
∴∠BAD=∠BAC+∠CAD=39°+39°=78°
(2)证明:∵EC=BC,
∴∠CEB=∠CBE,
而∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,
∴∠2+∠BAE=∠1+∠CBD,
∵∠BAE=∠BDC=∠CBD,
∴∠1=∠2
【解析】(1)根据等腰三角形的性质由BC=DC得到∠CBD=∠CDB=39°,再根据圆周角定理得∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,所以∠BAD=∠BAC+∠CAD=78°;(2)根据等腰三角形的性质由EC=BC得∠CEB=∠CBE,再利用三角形外角性质得∠CEB=∠2+∠BAE,则∠2+∠BAE=∠1+∠CBD,加上∠BAE=∠CBD,所以∠1=∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,画一个长和宽分别为
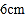 、
、 的长方形,并将其按一定的方式进行旋转.
的长方形,并将其按一定的方式进行旋转.
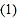 你能得到几种不同的圆柱体?
你能得到几种不同的圆柱体? 把一个平面图形旋转成几何体,必须明确哪两个条件?
把一个平面图形旋转成几何体,必须明确哪两个条件? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC与BD相交于O,∠1=∠4,∠2=∠3,△ABC的周长为25cm,△AOD的周长为17cm,则AB=( )
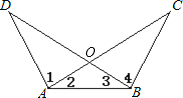
A. 4cm ; B. 8cm; C. 12cm; D. 无法确定;
-
科目: 来源: 题型:
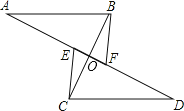
查看答案和解析>>【题目】如图,AB∥CD,CE∥BF,
A. E、F、D在一直线上,BC与AD交于点O,且OE=OF,则图中有全等三角形的对数为( )
A. 2
B. 3
C. 4
D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
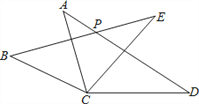
查看答案和解析>>【题目】如图,在△ACD和△BCE中,AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为 __________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平整的地面上,有若干个完全相同的棱长为10cm的小正方体堆成一个几何体,如图所示.
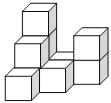
(1)这个几何体由 个小正方体组成,请画出这个几何体的三视图;
(2)如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有 个正方体只有一个面是黄色,有 个正方体只有两个面是黄色,有 个正方体只有三个面是黄色;
(3)若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加几个小正方体.
相关试题

