【题目】入冬以来,我省的雾霾天气频发,空气质量较差,容易引起多种上呼吸道疾病.某电器商场代理销售![]() ,
,![]() 两种型号的家用空气净化器,已知一台
两种型号的家用空气净化器,已知一台![]() 型空气净化器的进价比一台
型空气净化器的进价比一台![]() 型空气净化器的进价高200元;2台
型空气净化器的进价高200元;2台![]() 型空气净化器的进价与3台
型空气净化器的进价与3台![]() 型空气净化器的进价相同.
型空气净化器的进价相同.
(1)求![]() ,
,![]() 两种型号的家用空气净化器的进价分别是多少元.
两种型号的家用空气净化器的进价分别是多少元.
(2)若商场购进这两种型号的家用空气净化器共50台,其中![]() 型家用空气净化器的数量不超过
型家用空气净化器的数量不超过![]() 型家用空气净化器的数量,且不少于16台,设购进
型家用空气净化器的数量,且不少于16台,设购进![]() 型家用空气净化器
型家用空气净化器![]() 台.
台.
①求![]() 的取值范围;
的取值范围;
②已知![]() 型家用空气净化器的售价为每台800元,销售成本为每台
型家用空气净化器的售价为每台800元,销售成本为每台![]() 元;
元;![]() 型家用空气净化器的售价为每台550元,销售成本为每台
型家用空气净化器的售价为每台550元,销售成本为每台![]() 元.若
元.若![]() ,求售完这批家用空气净化器的最大利润
,求售完这批家用空气净化器的最大利润![]() (元)与
(元)与![]() (元)的函数关系式.(每台销售利润=售价-进价-销售成本)
(元)的函数关系式.(每台销售利润=售价-进价-销售成本)
参考答案:
【答案】(1)![]() 型进价600元/台,
型进价600元/台,![]() 型进价400元/台.(2)①
型进价400元/台.(2)①![]() 的取值范围为
的取值范围为![]() 且为整数.②
且为整数.②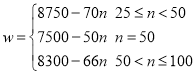
【解析】
(1)设![]() 型进价
型进价![]() 元/台,
元/台,![]() 型进价
型进价![]() 元/台,由题意得:
元/台,由题意得:![]() ,解方程组可得;(2)①由题意得:
,解方程组可得;(2)①由题意得:![]() ,②分段分析可得:
,②分段分析可得: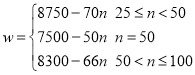 .
.
解:(1)设![]() 型进价
型进价![]() 元/台,
元/台,![]() 型进价
型进价![]() 元/台,
元/台,
由题意得:![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 型进价600元/台,
型进价600元/台,![]() 型进价400元/台.
型进价400元/台.
(2)①由题意得:![]() ,
,
∴![]() ,
,
∴![]() 的取值范围为
的取值范围为![]() 且为整数.
且为整数.
②由题意得:![]()
![]() .
.
∵![]() ,
,
1)当![]() 时,
时,![]() ,
,![]() 随着
随着![]() 的增大而增大,
的增大而增大,
∵![]() ,
,
∴当![]() 时,
时,![]() 最大,
最大,![]() .
.
2)当![]() 时,
时,![]() .
.
3)当![]() 时,
时,![]() ,
,![]() 随着
随着![]() 的增大而减小,
的增大而减小,
∴当![]() 时,
时,![]() 最大,
最大,![]() .
.
综上: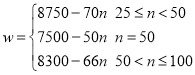 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
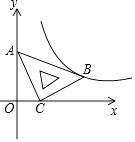
A.( ,0)
,0)
B.(2,0)
C.( ,0)
,0)
D.(3,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则sin∠PAP'的值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
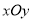 中,一次函数
中,一次函数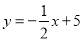 的图象
的图象 分别与
分别与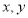 轴交于
轴交于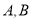 两点,正比例函数的图象
两点,正比例函数的图象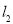 与
与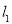 交于点
交于点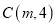
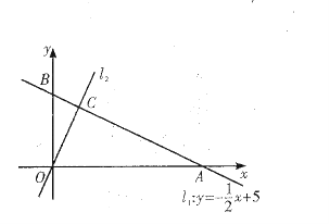
(1)求
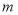 的值及
的值及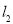 的解析式;
的解析式;(2)求
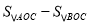 的值;
的值;(3)一次函数
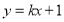 的图象为
的图象为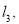 且
且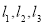 不能围成三角形,直接写出
不能围成三角形,直接写出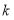 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】修建某一建筑时,若请甲、乙两个工程队同时施工,5天可以完成,需付两队费用共3 500元;若先请甲队单独做3天,再请乙队单独做6天可以完成,需付两队费用共3 300元.问:
(1)甲、乙两队每天的费用各为多少?
(2)若单独请某队完成工程,则单独请哪队施工费用较少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副含
 和
和  角的三角板
角的三角板  和
和  叠合在一起,边
叠合在一起,边  与
与  重合,
重合,  (如图1),点
(如图1),点  为边
为边 
 的中点,边
的中点,边  与
与  相交于点
相交于点  ,此时线段
,此时线段  的长是 . 现将三角板
的长是 . 现将三角板  绕点
绕点  按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在  从
从  到
到  的变化过程中,点
的变化过程中,点  相应移动的路径长共为 . (结果保留根号)
相应移动的路径长共为 . (结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(3,0),∠ABO=30°,且AB⊥BC.
(1)求直线BC和AB的解析式;
(2)将点B沿某条直线折叠到点O,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;
(3)在平面直角坐标系内是否存在两个点,使得这两个点与B、C两点构成的四边形是正方形?若存在,请求出这两点的坐标;若不存在,请说明理由.

相关试题

