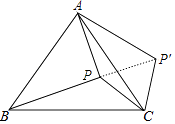
【题目】如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则sin∠PAP'的值为 . 
参考答案:
【答案】![]()
【解析】解:连接PP′,如图, ∵线段PC绕点C顺时针旋转60°得到P'C,
∴CP=CP′=6,∠PCP′=60°,
∴△CPP′为等边三角形,
∴PP′=PC=6,
∵△ABC为等边三角形,
∴CB=CA,∠ACB=60°,
∴∠PCB=∠P′CA,
在△PCB和△P′CA中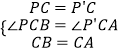 ,
,
∴△PCB≌△P′CA,
∴PB=P′A=10,
∵62+82=102 ,
∴PP′2+AP2=P′A2 ,
∴△APP′为直角三角形,∠APP′=90°,
∴sin∠PAP′= ![]() =
= ![]() =
= ![]() .
.
所以答案是 ![]() .
.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取
 =1.732,结果精确到1m)
=1.732,结果精确到1m)
-
科目: 来源: 题型:
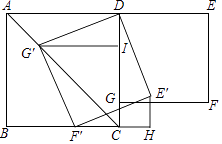
查看答案和解析>>【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )
A.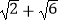
B.
C.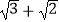
D.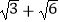
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
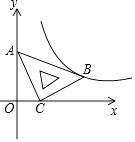
A.( ,0)
,0)
B.(2,0)
C.( ,0)
,0)
D.(3,0) -
科目: 来源: 题型:
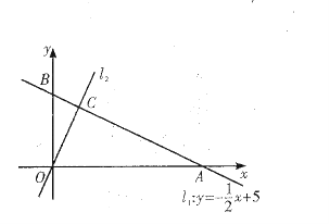
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,一次函数
中,一次函数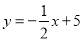 的图象
的图象 分别与
分别与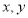 轴交于
轴交于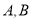 两点,正比例函数的图象
两点,正比例函数的图象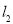 与
与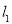 交于点
交于点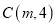
(1)求
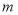 的值及
的值及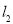 的解析式;
的解析式;(2)求
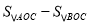 的值;
的值;(3)一次函数
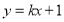 的图象为
的图象为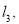 且
且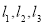 不能围成三角形,直接写出
不能围成三角形,直接写出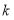 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】入冬以来,我省的雾霾天气频发,空气质量较差,容易引起多种上呼吸道疾病.某电器商场代理销售
 ,
,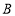 两种型号的家用空气净化器,已知一台
两种型号的家用空气净化器,已知一台 型空气净化器的进价比一台
型空气净化器的进价比一台 型空气净化器的进价高200元;2台
型空气净化器的进价高200元;2台 型空气净化器的进价与3台
型空气净化器的进价与3台 型空气净化器的进价相同.
型空气净化器的进价相同.(1)求
 ,
, 两种型号的家用空气净化器的进价分别是多少元.
两种型号的家用空气净化器的进价分别是多少元.(2)若商场购进这两种型号的家用空气净化器共50台,其中
 型家用空气净化器的数量不超过
型家用空气净化器的数量不超过 型家用空气净化器的数量,且不少于16台,设购进
型家用空气净化器的数量,且不少于16台,设购进 型家用空气净化器
型家用空气净化器 台.
台.①求
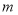 的取值范围;
的取值范围;②已知
 型家用空气净化器的售价为每台800元,销售成本为每台
型家用空气净化器的售价为每台800元,销售成本为每台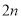 元;
元; 型家用空气净化器的售价为每台550元,销售成本为每台
型家用空气净化器的售价为每台550元,销售成本为每台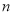 元.若
元.若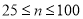 ,求售完这批家用空气净化器的最大利润
,求售完这批家用空气净化器的最大利润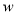 (元)与
(元)与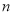 (元)的函数关系式.(每台销售利润=售价-进价-销售成本)
(元)的函数关系式.(每台销售利润=售价-进价-销售成本) -
科目: 来源: 题型:
查看答案和解析>>【题目】修建某一建筑时,若请甲、乙两个工程队同时施工,5天可以完成,需付两队费用共3 500元;若先请甲队单独做3天,再请乙队单独做6天可以完成,需付两队费用共3 300元.问:
(1)甲、乙两队每天的费用各为多少?
(2)若单独请某队完成工程,则单独请哪队施工费用较少?
相关试题

