【题目】如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(3,0),∠ABO=30°,且AB⊥BC.
(1)求直线BC和AB的解析式;
(2)将点B沿某条直线折叠到点O,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;
(3)在平面直角坐标系内是否存在两个点,使得这两个点与B、C两点构成的四边形是正方形?若存在,请求出这两点的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)y=![]() x+3
x+3![]() x,y=-
x,y=-![]() x+3
x+3![]() (2)点F(0,0)或(﹣3,0)(3)点M(﹣9﹣3
(2)点F(0,0)或(﹣3,0)(3)点M(﹣9﹣3![]() ,9),点N(﹣3
,9),点N(﹣3![]() ,9+3
,9+3![]() );点F(
);点F(![]() ,
,![]() ),点E坐标为(
),点E坐标为(![]() ,
,![]() )
)
【解析】
(1)根据题意可求点B,点C的坐标,用待定系数法可求解析式;(2)由题意可证DE是三角形的中位线,可求点D,点E的坐标,根据勾股定理可列方程,即可求点F的坐标;(3)分BC为边,BC为对角线讨论,根据正方形的性质,可求点的坐标.
(1)∵点A的坐标为(3,0)
∴AO=3
∵∠ABO=30°,∠AOB=90°
∴BO=![]() AO=3
AO=3![]() ,AB=2OA=6,∠OAB=60°,
,AB=2OA=6,∠OAB=60°,
又∵AB⊥BC
∴∠ACB=30°
∴AC=2AB=12
∴OC=AC﹣OA=12﹣3=9
∵OC=9,OB=3![]()
∴点B(0,3![]() ),点C(﹣9,0)
),点C(﹣9,0)
设直线BC解析式y=kx+b
![]() ,
,
解得:k=![]() ,b=3
,b=3![]()
∴直线BC解析式y=![]() x+3
x+3![]()
设直线AB解析式y=mx+n
![]() ,
,
解得:m=﹣![]() ,n=3
,n=3![]()
∴直线AB解析式y=﹣![]() x+3
x+3![]()
(2)
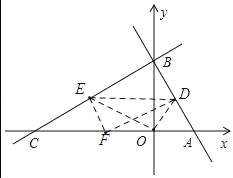
∵折叠,点O与点B重合
∴DE是BO的垂直平分线
∴EO=BE,BD=OD
∴∠EBO=∠EOB,∠DBO=∠DOB
∵BO⊥CO
∴∠EBO+∠ECO=90°,∠EOB+∠EOC=90°
∴∠EOC=∠ECO
∴CE=EO
∴CE=BE
同理BD=DA
∴DE=![]() AC=6
AC=6
∵点A(3,0),点B(0,3![]() ),点C(﹣9,0)
),点C(﹣9,0)
∴点E(﹣![]() ,
,![]() ),点D(
),点D(![]() ,
,![]() )
)
设点F(x,0)
∵△EFD是直角三角形,DE是斜边
∴DE2=EF2+DF2.
∴36=(x+![]() )2+
)2+![]() +(x﹣
+(x﹣![]() )2+
)2+![]()
解得:x1=0,x2=﹣3
∴点F(0,0)或(﹣3,0)
(3)若BC为边,在BC上方和下方作正方形,如图:四边形BCFE是正方形,四边形BCMN是正方形
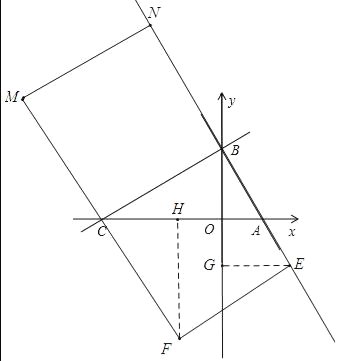
过点F作FH⊥AC于点H,过点E作EG⊥BO于点G
∵四边形BCFE是正方形
∴BC=CF,∠BCF=90°
∴∠BCO+∠FCH=90°,且∠FCH+∠CFH=90°
∴∠BCO=∠CFH且∠BOC=∠CHF=90°,BC=CF
∴△BCO≌△CFO(AAS)
∴CH=OB=3![]() ,HF=CO=9
,HF=CO=9
∴OH=9﹣3![]()
∴点F(﹣9+3![]() ,﹣9)
,﹣9)
同理可得△BEG≌△CBO
∴BG=CO=9,GE=BO=3![]()
∴OG=9﹣3![]()
∴点E(3![]() ,﹣9+3
,﹣9+3![]() )
)
同理可得:点M(﹣9﹣3![]() ,9),点N(﹣3
,9),点N(﹣3![]() ,9+3
,9+3![]() )
)
若BC为对角线,如图:四边形BECF是正方形
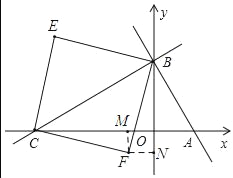
过点F作FM⊥CO于点M,作FN⊥BO于点 N
∵FM⊥CO,FN⊥BO,BO⊥CO
∴四边形OMFN是矩形
∴OM=FN,ON=FM
∵四边形BECF是正方形
∴CF=BF,∠CFB=90°
∵∠CFB=∠COB=90°
∴点C,点B,点O,点F四点共圆
∴∠FCO=∠OBF,且CF=BF,∠FMC=∠FNB=90°
∴△FMC≌△FNB(AAS)
∴FM=FN,CM=BN
∴边形FNOM是正方形
∴OM=ON=FM=FN
∵CM+OM=9,BN﹣ON=3![]()
∴OM=ON=![]() ,CM=BN=
,CM=BN=![]()
∴点F(![]() ,
,![]() )
)
同理可求点E坐标为(![]() ,
,![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】入冬以来,我省的雾霾天气频发,空气质量较差,容易引起多种上呼吸道疾病.某电器商场代理销售
 ,
, 两种型号的家用空气净化器,已知一台
两种型号的家用空气净化器,已知一台 型空气净化器的进价比一台
型空气净化器的进价比一台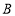 型空气净化器的进价高200元;2台
型空气净化器的进价高200元;2台 型空气净化器的进价与3台
型空气净化器的进价与3台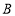 型空气净化器的进价相同.
型空气净化器的进价相同.(1)求
 ,
,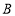 两种型号的家用空气净化器的进价分别是多少元.
两种型号的家用空气净化器的进价分别是多少元.(2)若商场购进这两种型号的家用空气净化器共50台,其中
 型家用空气净化器的数量不超过
型家用空气净化器的数量不超过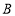 型家用空气净化器的数量,且不少于16台,设购进
型家用空气净化器的数量,且不少于16台,设购进 型家用空气净化器
型家用空气净化器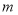 台.
台.①求
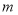 的取值范围;
的取值范围;②已知
 型家用空气净化器的售价为每台800元,销售成本为每台
型家用空气净化器的售价为每台800元,销售成本为每台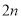 元;
元;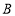 型家用空气净化器的售价为每台550元,销售成本为每台
型家用空气净化器的售价为每台550元,销售成本为每台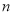 元.若
元.若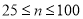 ,求售完这批家用空气净化器的最大利润
,求售完这批家用空气净化器的最大利润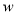 (元)与
(元)与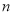 (元)的函数关系式.(每台销售利润=售价-进价-销售成本)
(元)的函数关系式.(每台销售利润=售价-进价-销售成本) -
科目: 来源: 题型:
查看答案和解析>>【题目】修建某一建筑时,若请甲、乙两个工程队同时施工,5天可以完成,需付两队费用共3 500元;若先请甲队单独做3天,再请乙队单独做6天可以完成,需付两队费用共3 300元.问:
(1)甲、乙两队每天的费用各为多少?
(2)若单独请某队完成工程,则单独请哪队施工费用较少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副含
 和
和  角的三角板
角的三角板  和
和  叠合在一起,边
叠合在一起,边  与
与  重合,
重合,  (如图1),点
(如图1),点  为边
为边 
 的中点,边
的中点,边  与
与  相交于点
相交于点  ,此时线段
,此时线段  的长是 . 现将三角板
的长是 . 现将三角板  绕点
绕点  按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在  从
从  到
到  的变化过程中,点
的变化过程中,点  相应移动的路径长共为 . (结果保留根号)
相应移动的路径长共为 . (结果保留根号)
-
科目: 来源: 题型:
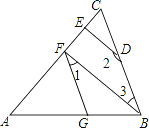
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
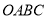 ,点
,点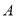 、
、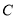 分别在
分别在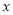 轴、
轴、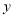 轴上, 点
轴上, 点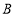 坐标为
坐标为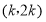 , 连接
, 连接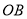 ,将矩形
,将矩形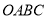 沿
沿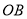 折叠,点
折叠,点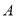 的对应点为点
的对应点为点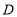 ,则点
,则点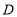 的坐标为_____(用含
的坐标为_____(用含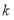 的式子表示).
的式子表示).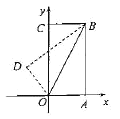
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是 .
相关试题

