【题目】一副含 ![]() 和
和 ![]() 角的三角板
角的三角板 ![]() 和
和 ![]() 叠合在一起,边
叠合在一起,边 ![]() 与
与 ![]() 重合,
重合, ![]() (如图1),点
(如图1),点 ![]() 为边
为边 ![]()
![]() 的中点,边
的中点,边 ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,此时线段
,此时线段 ![]() 的长是 . 现将三角板
的长是 . 现将三角板 ![]() 绕点
绕点 ![]() 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在 ![]() 从
从 ![]() 到
到 ![]() 的变化过程中,点
的变化过程中,点 ![]() 相应移动的路径长共为 . (结果保留根号)
相应移动的路径长共为 . (结果保留根号)
参考答案:
【答案】12( ![]() -1)cm;(12
-1)cm;(12 ![]() -18)cm
-18)cm
【解析】解:如图1,过H作HI⊥AC于I,
∵BC=EF=12cm,
∴AC=BC·tan∠ABC=![]() ×12=4
×12=4![]() cm,
cm,
∵∠BCD=45°,所以∠ACD=45°,
设HI=x,则IC=x,AI=![]() x,
x,
∵AC=AI+IC,
∴4![]() =
=![]() x+x,
x+x,
解得x=6(![]() -1),
-1),
则AH=![]() HI=12(1-
HI=12(1-![]() ),
),
∵AB=2AC=8![]()
∴BH=![]() =12(
=12(![]() )cm,
)cm,
所以答案是12(![]() )cm
)cm
如图2和图3,在 ∠ C G F 从 0 ° 到 60 ° 的变化过程中,点H先向AB方向移,在往BA方向移,直到H与F重合(下面证明此时∠CGF=60度),此时BH的值最大,
如图3,当F与H重合时,连接CF,因为BG=CG=GF,
所以∠BFC=90度,
∵∠B=30度,
∴∠BFC=60度,
由CG=GF可得∠CGF=60度.
∵BC=12cm,所以BF=![]() BC=6
BC=6![]() ;
;
如图2,当GH⊥DF时,GH有最小值,则BH有最小值,且GF//AB,连接DG,交AB于点K,则DG⊥AB,
∵DG=FG,
∴∠DGH=45度,
则KG=KH=![]() GH=
GH=![]() (
(![]() ×6
×6![]() )=3,
)=3,
BK=![]() KG=3
KG=3![]() ,
,
则BH=BK+KH=3![]() +3,
+3,
则点H运动的总路程为![]() (cm)
(cm)
所以答案是(![]() )cm
)cm

【考点精析】认真审题,首先需要了解旋转的性质(①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了).
-
科目: 来源: 题型:
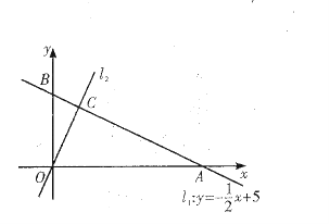
查看答案和解析>>【题目】如图,在平面直角坐标系
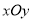 中,一次函数
中,一次函数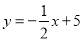 的图象
的图象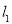 分别与
分别与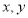 轴交于
轴交于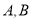 两点,正比例函数的图象
两点,正比例函数的图象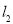 与
与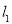 交于点
交于点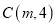
(1)求
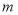 的值及
的值及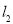 的解析式;
的解析式;(2)求
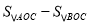 的值;
的值;(3)一次函数
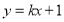 的图象为
的图象为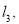 且
且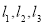 不能围成三角形,直接写出
不能围成三角形,直接写出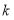 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】入冬以来,我省的雾霾天气频发,空气质量较差,容易引起多种上呼吸道疾病.某电器商场代理销售
 ,
,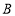 两种型号的家用空气净化器,已知一台
两种型号的家用空气净化器,已知一台 型空气净化器的进价比一台
型空气净化器的进价比一台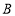 型空气净化器的进价高200元;2台
型空气净化器的进价高200元;2台 型空气净化器的进价与3台
型空气净化器的进价与3台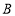 型空气净化器的进价相同.
型空气净化器的进价相同.(1)求
 ,
,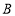 两种型号的家用空气净化器的进价分别是多少元.
两种型号的家用空气净化器的进价分别是多少元.(2)若商场购进这两种型号的家用空气净化器共50台,其中
 型家用空气净化器的数量不超过
型家用空气净化器的数量不超过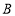 型家用空气净化器的数量,且不少于16台,设购进
型家用空气净化器的数量,且不少于16台,设购进 型家用空气净化器
型家用空气净化器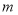 台.
台.①求
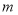 的取值范围;
的取值范围;②已知
 型家用空气净化器的售价为每台800元,销售成本为每台
型家用空气净化器的售价为每台800元,销售成本为每台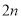 元;
元;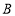 型家用空气净化器的售价为每台550元,销售成本为每台
型家用空气净化器的售价为每台550元,销售成本为每台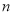 元.若
元.若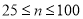 ,求售完这批家用空气净化器的最大利润
,求售完这批家用空气净化器的最大利润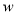 (元)与
(元)与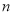 (元)的函数关系式.(每台销售利润=售价-进价-销售成本)
(元)的函数关系式.(每台销售利润=售价-进价-销售成本) -
科目: 来源: 题型:
查看答案和解析>>【题目】修建某一建筑时,若请甲、乙两个工程队同时施工,5天可以完成,需付两队费用共3 500元;若先请甲队单独做3天,再请乙队单独做6天可以完成,需付两队费用共3 300元.问:
(1)甲、乙两队每天的费用各为多少?
(2)若单独请某队完成工程,则单独请哪队施工费用较少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(3,0),∠ABO=30°,且AB⊥BC.
(1)求直线BC和AB的解析式;
(2)将点B沿某条直线折叠到点O,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;
(3)在平面直角坐标系内是否存在两个点,使得这两个点与B、C两点构成的四边形是正方形?若存在,请求出这两点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
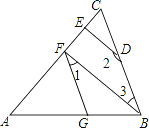
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
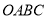 ,点
,点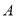 、
、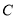 分别在
分别在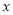 轴、
轴、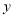 轴上, 点
轴上, 点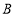 坐标为
坐标为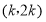 , 连接
, 连接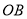 ,将矩形
,将矩形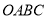 沿
沿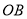 折叠,点
折叠,点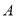 的对应点为点
的对应点为点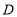 ,则点
,则点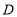 的坐标为_____(用含
的坐标为_____(用含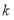 的式子表示).
的式子表示).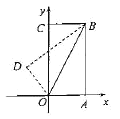
相关试题

