搜索
【题目】如图，已知抛物线y=﹣x2+bx+c与x轴交于点A（﹣1，0）和点B（3，0），与y轴交于点C，连接BC交抛物线的对称轴于点E，D是抛物线的顶点．
（1）求此抛物线的解析式；
（2）直接写出点C和点D的坐标；
（3）若点P在第一象限内的抛物线上，且S△ABP=4S△COE ， 求P点坐标．
参考答案：
【答案】
（1）解：由点A（﹣1，0）和点B（3，0）得： 
，解得： 
，∴抛物线的解析式为 
（2）解： 令x=0，则y=3，∴C（0，3），∵ =﹣（x﹣1）2+4，∴D（1，4）
（3）解：设P（x，y）（x＞0，y＞0），S△COE= 
×1×3= 
，S△ABP= ×4y=2y，∵S△ABP=4S△COE，∴2y=4× ，∴y=3，∴﹣x2+2x+3=3，解得：x1=0（不合题意，舍去），x2=2，∴P（2，3）
【解析】（1）用待定系数法把A、点B的坐标代入求出抛物线的解析式；（2）根据与y轴交于点C，求出点C的坐标，根据顶点式求出点D的坐标；（3）根据三角形的面积公式求出P点坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球（除颜色不同外，其它都一样），其中红球2个，蓝球1个，现在从中任意摸出一个红球的概率为
．
（1）求袋中黄球的个数；
（2）第一次摸出一个球（不放回），第二次再摸出一个球，请用树状图或列表法求两次摸出的都是红球的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】某校拟派一名跳高运动员参加校际比赛，对甲、乙两名同学进行了8次跳高选拔比赛，他们的原始成绩（单位：cm）如下表：
学生/成绩/次数
第1次
第2次
第3次
第4次
第5次
第6次
第7次
第8次
甲
169
165
168
169
172
173
169
167
乙
161
174
172
162
163
172
172
176
两名同学的8次跳高成绩数据分析如下表：
学生/成绩/名称
平均数（单位：cm）
中位数（单位：cm）
众数（单位：cm）
方差（单位：cm2）
甲
a
b
c
5.75
乙
169
172
172
31.25
根据图表信息回答下列问题：
（1）a＝ ，b＝ ，c＝ ；
（2）这两名同学中， 的成绩更为稳定；（填甲或乙）
（3）若预测跳高165就可能获得冠军，该校为了获取跳高比赛冠军，你认为应该选择 同学参赛，理由是： ；
（4）若预测跳高170方可夺得冠军，该校为了获取跳高比赛冠军，你认为应该选择 同学参赛，班由是： ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了加强公民的节水意识，合理利用水资源，某市采用价格调控手段达到节水的目的．该市自来水收费价格见价目表．
若某户居民
月份用水
，则应收水费：
元．（1）若该户居民
月份用水
，则应收水费______元；（2）若该户居民
、
月份共用水
（月份用水量超过月份），共交水费
元，则该户居民，月份各用水多少立方米？ -
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面的证明，在括号内填上理由．
如图，
，
． 求证：
．证明：
（已知），
（____________________）．
（____________________）．
__________
（____________________）．
（____________________）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，BC是⊙O的弦，半径OD⊥BC，垂足为E，若BC=
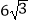，DE=3．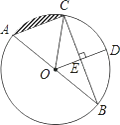
求：
（1）⊙O的半径；
（2）弦AC的长；
（3）阴影部分的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图某幢大楼顶部有广告牌CD．张老师目高MA为1.60米，他站立在离大楼45米的A处测得大楼顶端点D的仰角为30°；接着他向大楼前进14米、站在点B处，测得广告牌顶端点C的仰角为45°．（取
,计算结果保留一位小数）
（1）求这幢大楼的高DH；
（2）求这块广告牌CD的高度．
相关试题
