【题目】如图某幢大楼顶部有广告牌CD.张老师目高MA为1.60米,他站立在离大楼45米的A处测得大楼顶端点D的仰角为30°;接着他向大楼前进14米、站在点B处,测得广告牌顶端点C的仰角为45°.(取 ![]() ,计算结果保留一位小数)
,计算结果保留一位小数)
(1)求这幢大楼的高DH;
(2)求这块广告牌CD的高度.
参考答案:
【答案】
(1)解:在Rt△DME中,ME=AH=45米;
由tan30°= ![]() ,得DE=45×
,得DE=45× ![]() =15×1.732=25.98米;
=15×1.732=25.98米;
又因为EH=MA=1.6米,因而大楼DH=DE+EH=25.98+1.6=27.58≈27.6米
(2)解:又在 Rt△CNE中,NE=45﹣14=31米,由tan45°= ![]() ,得CE=NE=31米;
,得CE=NE=31米;
因而广告牌CD=CE﹣DE=31﹣25.98≈5.0米;
答:楼高DH为27.6米,广告牌CD的高度为5.0米
【解析】(1)根据矩形的性质和解直角三角形求出这幢大楼的高DH;(2)根据特殊角的三角函数值求出CE=NE的值,得到广告牌CD=CE﹣DE的值.
【考点精析】认真审题,首先需要了解关于仰角俯角问题(仰角:视线在水平线上方的角;俯角:视线在水平线下方的角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.

(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE , 求P点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明,在括号内填上理由.
如图,
 ,
, .
. 求证:
 .
.证明:
 (已知),
(已知), (____________________).
(____________________). (____________________).
(____________________). __________
__________ (____________________).
(____________________). (____________________).
(____________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=
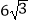 ,DE=3.
,DE=3.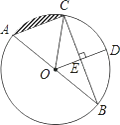
求:
(1)⊙O的半径;
(2)弦AC的长;
(3)阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)4+3(x-2)=x.
(2)
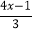 =1-
=1-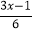 .
.(3)
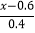 +x=
+x=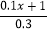 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内部,∠BOE=
 ∠EOC,∠DOE=70°,求∠EOC的度数.
∠EOC,∠DOE=70°,求∠EOC的度数.
相关试题

