【题目】已知数轴上有两点![]() ,
,![]() 对应的数分别为
对应的数分别为![]() ,
,![]() ,点
,点![]() 为数轴上一动点,对应点的数为
为数轴上一动点,对应点的数为![]() .
.
(1)若点![]() 到点
到点![]() ,点
,点![]() 的距离相等,则点
的距离相等,则点![]() 对应的数为________.
对应的数为________.
(2)数轴上是否存在点![]() ,使点
,使点![]() 到点
到点![]() 、点
、点![]() 的距离之和为8?若存在,请求出
的距离之和为8?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)当点![]() 以每秒
以每秒![]() 的单位长度的速度从
的单位长度的速度从![]() (原点)向左运动,同时点
(原点)向左运动,同时点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动,点
个单位长度的速度向左运动,点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动,问它们同时出发,几秒后点
个单位长度的速度向左运动,问它们同时出发,几秒后点![]() 到点
到点![]() 、点
、点![]() 的距离相等?
的距离相等?
参考答案:
【答案】(1)1;(2)-3或5;(3)![]() 秒或
秒或![]() 秒
秒
【解析】
(1)根据题意列方程即可得到结论;
(2)利用当A在M左侧时,当A在N右侧时,分别得出即可;
(3)利用当A点在M、N之间时,此时N到A点距离等于M点到A点距离,以及当A点在M、N右侧时,此时M、N重合,求出即可.
解:(1)根据题意得,a-(-2)=4-a,
∴a=1,
故答案为:1;
(2)存在,
∵点A到点M、点N的距离之和为8,
∴|a+2|+|a-4|=8,
当a≤-2时,原方程可化为:-a-2+4-a=8,解得a=-3;
当-2<a<4时,原方程可化为:a+2+4-a=8,则4=5(舍)
当a≥4时,原方程可化为:a+2+a-4=8,解得a=5;
综上:点A对应的数为-3或5时,它到点M、点N的距离之和为8;
(3)设同时出发x秒后点A到点M、点N的距离相等.
①点A在点M与点N之间,
根据题意,得
10x+2-2x=2x+4-40x,
解得x= ![]() ;
;
②点N追上点M时,根据题意得
40x-10x=6,
解得x=![]() ,
,
答:同时出发![]() 秒或
秒或![]() 秒后点A到点M、点N的距离相等.
秒后点A到点M、点N的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=
 ,求AF的长.
,求AF的长.
-
科目: 来源: 题型:
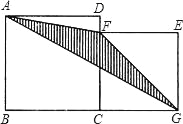
查看答案和解析>>【题目】如图所示,四边形ABCD和CGEF分别是边长为xcm和ycm的正方形,
(1)用含x和y的代数式表示图中阴影部分的面积.
(2)当x=24,y=20时,求此阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量
 的取值范围;
的取值范围;(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=-
 x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.(1)若点C在反比例函数y=
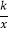 的图象上,求该反比例函数的解析式;
的图象上,求该反比例函数的解析式;(2)点P(2
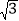 ,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,P点是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.
,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,P点是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.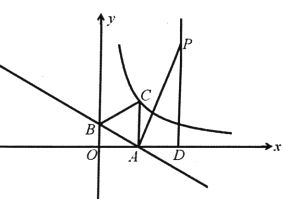
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六个完全相同的小矩形排成一个大矩形,AB是其中一个小矩形的对角线,请在大矩形中完成下列画图,要求:①仅用无刻度直尺②保留必要的作图痕迹.
(1)在如图中画出与线段AB平行的线段CD
(2)在如图中画出过点A与线段AB垂直的线段AE
(3)在如图中画出线段AB的垂直平分线MN


-
科目: 来源: 题型:
查看答案和解析>>【题目】 完成下面的证明.
如图,已知AB∥CD∥EF, 写出∠A,∠C,∠AFC的关系并说明理由.
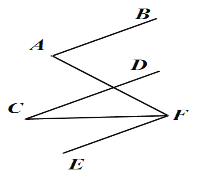
解:∠AFC= . 理由如下:
∵AB∥EF(已知),
∴∠A= (两直线平行,内错角相等).
∵CD∥EF(已知),
∴∠C= ( ).
∵∠AFC= - ,
∴∠AFC= (等量代换).
相关试题

