【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
参考答案:
【答案】(1)y=60+10x,x为x≤12的正整数.
(2)当超市降价3元时,即每箱33元时,所获利润最大,最大利润为810元.
【解析】试题分析:(1)根据价格每降低1元,平均每天多销售10箱,由每箱降价x元,多卖10x,据此可以列出函数关系式;(2)由利润=(售价﹣成本)×销售量列出函数关系式,求出最大值.
试题解析:(1)根据题意,得:y=60+10x,由36﹣x≥24得x≤12,
∴1≤x≤12,且x为整数;
(2)设所获利润为W,
则W=(36﹣x﹣24)(10x+60)=﹣10x2+60x+720=﹣10(x﹣3)2+810,
∴当x=3时,W取得最大值,最大值为810,
答:超市定价为33元时,才能使每月销售牛奶的利润最大,最大利润是810元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某长方形广场的四个角都有一个半径相同的四分之一圆形的草地,若圆形的半径为x米,长方形长为a米,宽为b米
(1)分别用代数式表示草地和空地的面积;
(2)若长方形长为300米,宽为200米,圆形的半径为10米,求广场空地的面积(计算结果保留到整数)

-
科目: 来源: 题型:
查看答案和解析>>【题目】一副含30°和45°角的三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12cm(如图1),点G为边BC(EF)的中点,边FD与AB相交于点H,此时线段BH的长是____.现将三角板DEF绕点G按顺时针方向旋转(如图2),在∠CGF从0°到60°的变化过程中,点H相应移动的路径长共为_________.(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=
 .
.(1)写出此二次函数图象的对称轴;
(2)在如图中建立平面直角坐标系,并画出该函数的图象.(列表、描点、连线)
(3)结合图象回答问题:
①当x的取值范围是 时,y≤0?
②将此抛物线向 平移 个单位时,它与x轴有且只有一个公共点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 (a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3.
(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3.
(1)求A、B两点的坐标;
(2)若tan∠PDB=
 ,求这个二次函数的关系式.
,求这个二次函数的关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是
是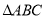 的外接圆,
的外接圆,  点在
点在 边上,
边上, 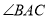 的平分线交
的平分线交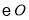 于点
于点 ,连接
,连接 ,过点
,过点 作
作 的平行线,与
的平行线,与 的延长线相交于点
的延长线相交于点 .
.(1)求证:
 是
是 的切线;
的切线;(2)求证:△PBD∽△DCA;
(3)当
 时,求线段
时,求线段 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地电话拨号入网有两种收费方式,用户可以任选其一.
计时制:0.05元/分;
包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网的时间为x小时,请你分别写出两种收费方式下该用户应该支付的费用.
(2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
相关试题

