【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=![]() ,求AF的长.
,求AF的长.

参考答案:
【答案】(1)证明见解析;(2). AF=2![]() .
.
【解析】
试题分析:(1)由平行四边形的性质得出AB∥CD,AD∥BC,AD=BC,得出∠D+∠C=180°,∠ABF=∠BEC,证出∠C=∠AFB,即可得出结论;(2)由勾股定理求出BE,由三角函数求出AE,再由相似三角形的性质求出AF的长.
试题解析:(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,AD=BC,
∴∠D+∠C=180°,∠ABF=∠BEC,∵∠AFB+∠AFE=180°,∴∠C=∠AFB,∴△ABF∽△BEC;
(2)解:∵AE⊥DC,AB∥DC,∴∠AED=∠BAE=90°,
在Rt△ABE中,根据勾股定理得:BE=![]() ,
,
在Rt△ADE中,AE=ADsinD=5×![]() =4,∵BC=AD=5,
=4,∵BC=AD=5,
由(1)得:△ABF∽△BEC,∴![]() ,即
,即![]() ,解得:AF=2
,解得:AF=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘轮船早上8时从点A向正北方向出发,小岛P在轮船的北偏西15°方向,轮船每小时航行15海里,11时轮船到达点B处,小岛P此时在轮船的北偏西30°方向.
(1)求此时轮船距小岛为多少海里?
(2)在小岛P的周围20海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,
 ,
, ,
, 是等腰直角三角形,且
是等腰直角三角形,且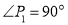 ,把
,把 绕点
绕点 顺时针旋转
顺时针旋转 ,得到
,得到 ;把
;把 绕点
绕点 顺时针旋转
顺时针旋转 ,得到
,得到 .依次类推,则旋转第2017次后,得到的等腰直角三角形的直角顶点
.依次类推,则旋转第2017次后,得到的等腰直角三角形的直角顶点 的坐标为( )
的坐标为( )
A.
 B.
B. C.
C.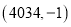 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
 中,
中, 的平分线交
的平分线交 于点
于点 ,交
,交 的延长线于点
的延长线于点 ,
,
(1)写出
 对由条件
对由条件 推出的相等或互补的角
推出的相等或互补的角(2)
 与
与 相等吗?为什么?
相等吗?为什么?(3)证明:

请在下面的括号内,填上推理的根据,并完成下面的证明:
 ( ① )
( ① ) (已证),
(已证), ,( ② )
,( ② )又
 (角平分线的定义)
(角平分线的定义) ( ③ )
( ③ )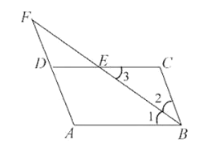
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=
 图象的两个交点.
图象的两个交点.(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣
 >0的解集.
>0的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,
, 是
是 的中点,点
的中点,点 在边
在边 上,将
上,将 沿
沿 翻折,使点
翻折,使点 落在点
落在点 处,当
处,当 时,
时, ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为﹣5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为
 BC的点N,则该数轴的原点为( )
BC的点N,则该数轴的原点为( )
A. 点E B. 点F C. 点M D. 点N
相关试题

