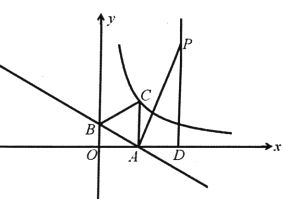
【题目】如图,一次函数y=-![]() x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
(1)若点C在反比例函数y=![]() 的图象上,求该反比例函数的解析式;
的图象上,求该反比例函数的解析式;
(2)点P(2![]() ,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,P点是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.
,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,P点是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.
参考答案:
【答案】![]()
![]() ;
; ![]() P点坐标为
P点坐标为![]()
【解析】试题分析:(1)由直线解析式可求得A、B坐标,在Rt△AOB中,利用三角函数定义可求得∠BAO=30°,且可求得AB的长,从而可求得CA⊥OA,则可求得C点坐标,利用待定系数法可求得反比例函数解析式;
(2)分△PAD∽△ABO和△PAD∽△BAO两种情况,分别利用相似三角形的性质可求得m的值,可求得P点坐标,代入反比例函数解析式进行验证即可.
试题解析:解:(1)在![]() 中,令y=0可解得x=
中,令y=0可解得x=![]() ,令x=0可得y=1,∴A(
,令x=0可得y=1,∴A(![]() ,0),B(0,1),∴tan∠BAO=
,0),B(0,1),∴tan∠BAO=![]() ,∴∠BAO=30°,∵△ABC是等边三角形,∴∠BAC=60°,∴∠CAO=90°,在Rt△BOA中,由勾股定理可得AB=2,∴AC=2,∴C(
,∴∠BAO=30°,∵△ABC是等边三角形,∴∠BAC=60°,∴∠CAO=90°,在Rt△BOA中,由勾股定理可得AB=2,∴AC=2,∴C(![]() ,2),∵点C在反比例函数
,2),∵点C在反比例函数![]() 的图象上,∴k=2×
的图象上,∴k=2×![]() =
=![]() ,∴反比例函数解析式为
,∴反比例函数解析式为![]() ;
;
(2)∵P(![]() ,m)在第一象限,∴AD=OD﹣OA=
,m)在第一象限,∴AD=OD﹣OA=![]() ﹣
﹣![]() =
=![]() ,PD=m,当△ADP∽△AOB时,则有
,PD=m,当△ADP∽△AOB时,则有![]() ,即
,即![]() ,解得m=1,此时P点坐标为(
,解得m=1,此时P点坐标为(![]() ,1);
,1);
当△PDA∽△AOB时,则有![]() ,即
,即![]() ,解得m=3,此时P点坐标为(
,解得m=3,此时P点坐标为(![]() ,3);
,3);
把P(![]() ,3)代入
,3)代入![]() 可得3≠
可得3≠![]() ,∴P(
,∴P(![]() ,3)不在反比例函数图象上,把P(
,3)不在反比例函数图象上,把P(![]() ,1)代入反比例函数解析式得1=
,1)代入反比例函数解析式得1=![]() ,∴P(
,∴P(![]() ,1)在反比例函数图象上;
,1)在反比例函数图象上;
综上可知P点坐标为(![]() ,1).
,1).
-
科目: 来源: 题型:
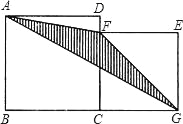
查看答案和解析>>【题目】如图所示,四边形ABCD和CGEF分别是边长为xcm和ycm的正方形,
(1)用含x和y的代数式表示图中阴影部分的面积.
(2)当x=24,y=20时,求此阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量
 的取值范围;
的取值范围;(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有两点
 ,
, 对应的数分别为
对应的数分别为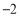 ,
,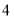 ,点
,点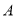 为数轴上一动点,对应点的数为
为数轴上一动点,对应点的数为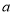 .
.(1)若点
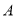 到点
到点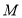 ,点
,点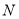 的距离相等,则点
的距离相等,则点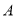 对应的数为________.
对应的数为________.(2)数轴上是否存在点
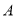 ,使点
,使点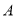 到点
到点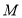 、点
、点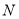 的距离之和为8?若存在,请求出
的距离之和为8?若存在,请求出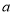 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(3)当点
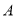 以每秒
以每秒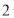 的单位长度的速度从
的单位长度的速度从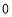 (原点)向左运动,同时点
(原点)向左运动,同时点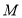 以每秒
以每秒 个单位长度的速度向左运动,点
个单位长度的速度向左运动,点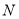 以每秒
以每秒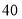 个单位长度的速度向左运动,问它们同时出发,几秒后点
个单位长度的速度向左运动,问它们同时出发,几秒后点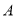 到点
到点 、点
、点 的距离相等?
的距离相等? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六个完全相同的小矩形排成一个大矩形,AB是其中一个小矩形的对角线,请在大矩形中完成下列画图,要求:①仅用无刻度直尺②保留必要的作图痕迹.
(1)在如图中画出与线段AB平行的线段CD
(2)在如图中画出过点A与线段AB垂直的线段AE
(3)在如图中画出线段AB的垂直平分线MN


-
科目: 来源: 题型:
查看答案和解析>>【题目】 完成下面的证明.
如图,已知AB∥CD∥EF, 写出∠A,∠C,∠AFC的关系并说明理由.
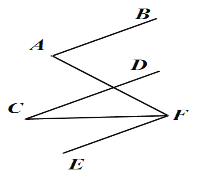
解:∠AFC= . 理由如下:
∵AB∥EF(已知),
∴∠A= (两直线平行,内错角相等).
∵CD∥EF(已知),
∴∠C= ( ).
∵∠AFC= - ,
∴∠AFC= (等量代换).
-
科目: 来源: 题型:
查看答案和解析>>【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
相关试题

