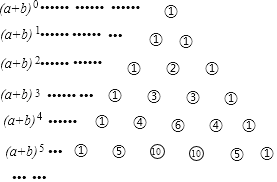
【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如下的三角形解释(a+b)n的展开式中各项的系数,此三角形称为“杨辉三角”,
即:(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
根据“杨辉三角”计算出(a+b)10的展开式中第三项的系数为( )
A.10B.45C.46D.50
参考答案:
【答案】B
【解析】
根据题意先得出![]() 的第三项的系数,观察这些系数的特点,由此进一步归纳总结出
的第三项的系数,观察这些系数的特点,由此进一步归纳总结出![]() 的第三项系数为
的第三项系数为![]() ,据此进一步得出答案即可.
,据此进一步得出答案即可.
由题意得:
![]() 的第三项的系数为:
的第三项的系数为:![]() ,
,
![]() 的第三项的系数为:
的第三项的系数为:![]() ,
,
![]() 的第三项的系数为:
的第三项的系数为:![]() ,
,
∴![]() 的第三项的系数为:
的第三项的系数为:![]() ,
,
∴![]() 的第三项系数为:
的第三项系数为:![]() ,
,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家推行“节能减排,低碳经济”政策后,某环保节能设备生产的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于44万元,每套产品的售价不低于80万元.已知这种设备的月产量x(套)与每套的售价y1(万元)间满足关系式y1=160﹣2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
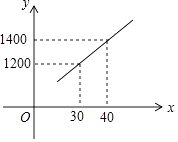
(1)直接写出y2与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程(或方程组)解应用题:
(1)某服装店到厂家选购甲、乙两种服装,若购进甲种服装9件、乙种服装10件,需1810元;购进甲种服装11件乙种服装8件,需1790元,求甲乙两种服装每件价格相差多少元?
(2)某工厂现库存某种原料1200吨,用来生产A、B两种产品,每生产1吨A产品需这种原料2吨、生产费用1000元;每生产1吨B产品需这种原料2.5吨、生产费用900元,如果用来生产这两种产品的资金为53万元,那么A、B两种产品各生产多少吨才能使库存原料和资金恰好用完?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一般地,
 个相同的因数
个相同的因数 相乘
相乘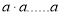 ,记为
,记为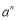 , 如
, 如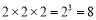 ,此时,3叫做以2为底8的对数,记为
,此时,3叫做以2为底8的对数,记为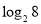 (即
(即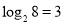 ) .一般地,若
) .一般地,若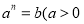 且
且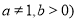 , 则
, 则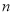 叫做以
叫做以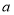 为底
为底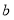 的对数, 记为
的对数, 记为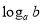 (即
(即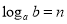 ) .如
) .如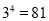 , 则4叫做以3为底81的对数, 记为
, 则4叫做以3为底81的对数, 记为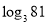 (即
(即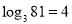 ) .
) .(1)计算下列各对数的值:
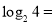 ;
;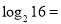 ;
;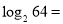 .
.(2)观察(1)中三数4、16、64之间满足怎样的关系式,
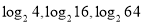 之间又满足怎样的关系式;
之间又满足怎样的关系式;(3)由(2)的结果,你能归纳出一个一般性的结论吗?
(4) 根据幂的运算法则:
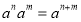 以及对数的含义说明上述结论.
以及对数的含义说明上述结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:P、Q分别是两条线段a,b上任意一点,线段PQ长度的最小值叫做线段a与线段b的距离.已知,O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角坐标系中四点.
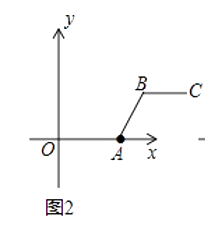
(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离为;当m=5,n=2时,如图2,线段BC与线段OA的距离(即线段AB的长)为;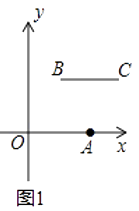
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.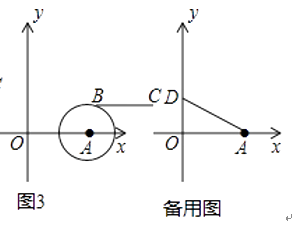
(3)当m值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M,点D(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m值,使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m值;若不存在,请说明理由. -
科目: 来源: 题型:
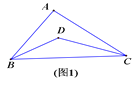
查看答案和解析>>【题目】(1)如图(1)所示,已知
 中,
中, 试确定
试确定
(2)如图(2)所示,已知
 中,
中, 试确定
试确定
(3)如图(3)所示,已知
 中,
中, 试确定
试确定


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C1:y=﹣
 x2+bx+c的对称轴是x=2,且经过点(6,0).
x2+bx+c的对称轴是x=2,且经过点(6,0).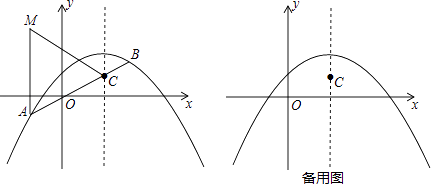
(1)求抛物线C1的解析式;
(2)将抛物线C1向下平移2个单位后得到抛物线C2 , 如图,直线y=kx﹣2k+1交抛物线C2于A,B两点(点A在点B的左边),交抛物线C2的对称轴于点C,M(xA , 3),xA表示点A横坐标,求证:AC=AM;
(3)在(2)的条件下,请你参考(2)中的结论解决下列问题:
①若CM=AM,求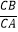 的值;
的值;
②请你探究:在抛物线C2上是否存在点P,使得PO+PC取得最小值?如果存在,求出点P的坐标;如果不存在,请说明理由.
相关试题

